filmov
tv
L07.3 Conditional Expectation & the Total Expectation Theorem

Показать описание
MIT RES.6-012 Introduction to Probability, Spring 2018
Instructor: John Tsitsiklis
License: Creative Commons BY-NC-SA
Instructor: John Tsitsiklis
License: Creative Commons BY-NC-SA
L07.3 Conditional Expectation & the Total Expectation Theorem
L13.2 Conditional Expectation as a Random Variable
The Conditional Expectation of X given that Y=y
L07.2 Conditional PMFs
Lecture 26 Conditional Expectation + Sum of Two Random Variables
L09.3 Conditioning Example
L07.5 Example
L06.4 Conditional PMFs & Expectations Given an Event
[Chapter 7] #5 Conditional expectation
Conditional Variance: Example 1
MA 381: Section 8.3: Conditional Probability Density Function for Continuous Random Variables
eco420 L07 3
Probability Video 4.5: Pairs of Random Variables - Conditional Expectation
Joint Distributions(3): Conditioning for Expected Values and Variances
computing conditional expectations 03 conditional expectation given a simple sigma algebra
L07.8 The Hat Problem
Probabilistic Analysis - Lecture 36 (IE 523)
Conditioning on Continuous Random Variables
Probability 4.7 Conditional Expectation (2022)
S07.3 Independence of Random Variables Versus Independence of Events
Proof: Mean Independence Implies Uncorrelatedness
Abstract Bayes' Formula and Conditional Expectation
08-09. Conditional expectation - Conditioning: the matching rounds problem.
mod09lec71 - Conditional Expectation
Комментарии
 0:06:10
0:06:10
 0:04:31
0:04:31
 0:04:11
0:04:11
 0:10:48
0:10:48
 0:47:49
0:47:49
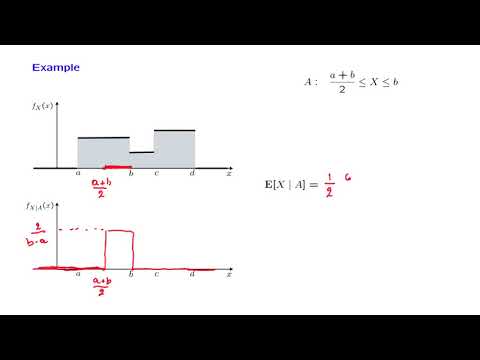 0:03:08
0:03:08
 0:04:44
0:04:44
 0:07:31
0:07:31
![[Chapter 7] #5](https://i.ytimg.com/vi/cTei-xg1om0/hqdefault.jpg) 0:03:24
0:03:24
 0:08:48
0:08:48
 0:07:18
0:07:18
 0:09:33
0:09:33
 0:25:40
0:25:40
 0:15:34
0:15:34
 0:11:36
0:11:36
 0:16:09
0:16:09
 0:49:42
0:49:42
 0:06:52
0:06:52
 0:17:43
0:17:43
 0:06:51
0:06:51
 0:06:10
0:06:10
 0:35:34
0:35:34
 0:22:00
0:22:00
 0:24:56
0:24:56