filmov
tv
Solving Integrals is the First sin(sin(sin(sin(sin(...))))) of Madness
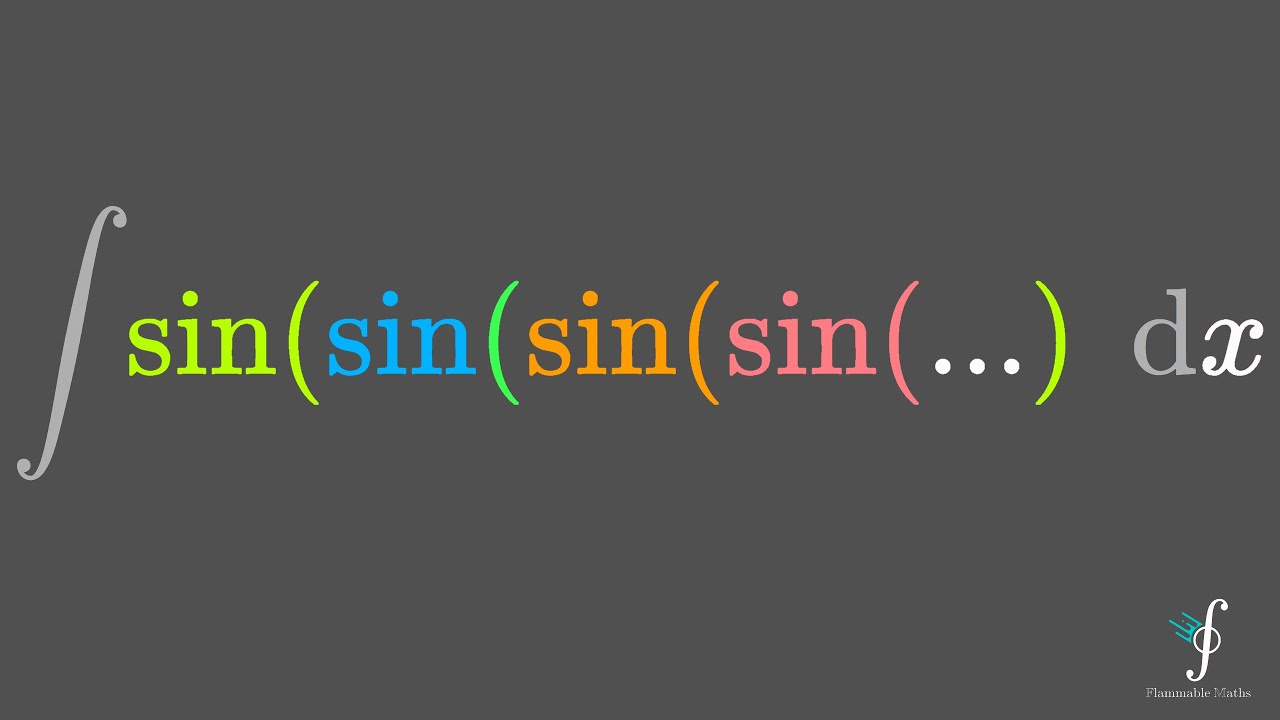
Показать описание
Subscribe to @RockHardWoodDaddy for DIY Videos and more! :D
Today we evaluate infinitely nested, recursively defined integrals of sine, cosine, tan, exponential function and the natural logarithm :) The Dottie Number and Lambert W function make an appearance and we find out some curious facts about the convergence of these functions to their respective fixed point equations. Enjoy! =D
Help me create more free content! =)
--------------------------------------------------------------------------------
Wanna send me some stuff? lel:
Postfach 11 15
06731 Bitterfeld-Wolfen
Saxony-Anhalt
Germany
--------------------------------------------------------------------------------
Today we evaluate infinitely nested, recursively defined integrals of sine, cosine, tan, exponential function and the natural logarithm :) The Dottie Number and Lambert W function make an appearance and we find out some curious facts about the convergence of these functions to their respective fixed point equations. Enjoy! =D
Help me create more free content! =)
--------------------------------------------------------------------------------
Wanna send me some stuff? lel:
Postfach 11 15
06731 Bitterfeld-Wolfen
Saxony-Anhalt
Germany
--------------------------------------------------------------------------------
Integration (Calculus)
Solving Integrals is the First sin(sin(sin(sin(sin(...))))) of Madness
Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus
Calculus 1 - Integration & Antiderivatives
Introduction to integral calculus | Accumulation and Riemann sums | AP Calculus AB | Khan Academy
100 integrals (world record?)
Double and Triple Integrals
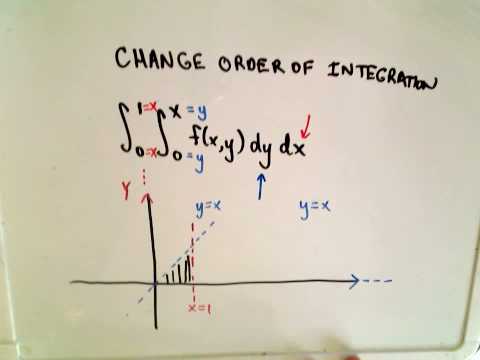
Evaluate the integral by reversing the order of integration
Find the definite integral of x*sqrt(x-1) on [1,2]: u-substitution and transforming the limits.
Calculus 3: Line Integrals (18 of 44) What is a Line Integral? [(y)dx+(z)dy+(x)dz] Example 6
Double Integrals
Basic Integration Using Power Formula
Definite Integral
Evaluating Surface Integrals
Double Integrals over General Regions Practice Problems
What is Integration by Parts - How to do Integration by Parts
INTEGRATION IMPORTANT QUESTION | CBSE BOARDS | CLASS 12 MATHS | STATE BOARDS | CUET #shorts_
Believe in double integral, NOT single integral
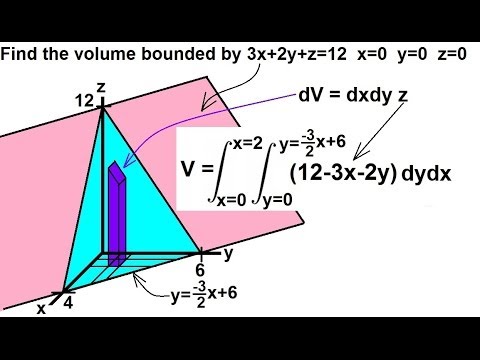
Calculus - Integration: Double Integrals (7 of 9) Example 6: Finding the Volume
Type 1 improper integrals! calculus 2
How to Find a Definite Integral using Riemann Sums and the Limit Definition: Quadratic Example
❖ Double Integrals - Changing Order of Integration ❖
Line Integrals - Evaluating a Line Integral
Improper Integrals - Convergence and Divergence - Calculus 2
Комментарии
 0:07:04
0:07:04
 0:14:51
0:14:51
 0:20:46
0:20:46
 0:40:04
0:40:04
 0:04:52
0:04:52
 5:50:23
5:50:23
 0:15:29
0:15:29
 0:08:15
0:08:15
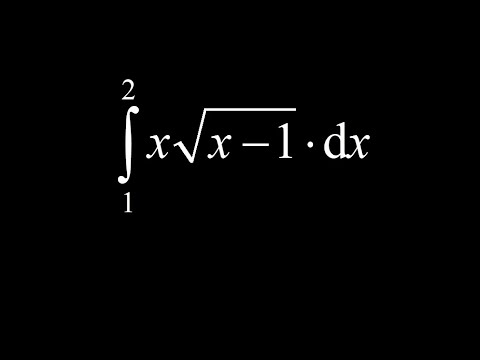 0:03:08
0:03:08
 0:05:03
0:05:03
 0:25:02
0:25:02
 0:20:41
0:20:41
 0:11:05
0:11:05
 0:12:24
0:12:24
 0:11:10
0:11:10
 0:03:57
0:03:57
 0:00:33
0:00:33
 0:11:14
0:11:14
 0:10:42
0:10:42
 0:27:48
0:27:48
 0:13:18
0:13:18
 0:04:20
0:04:20
 0:08:24
0:08:24
 0:13:56
0:13:56