filmov
tv
Find the definite integral of x*sqrt(x-1) on [1,2]: u-substitution and transforming the limits.
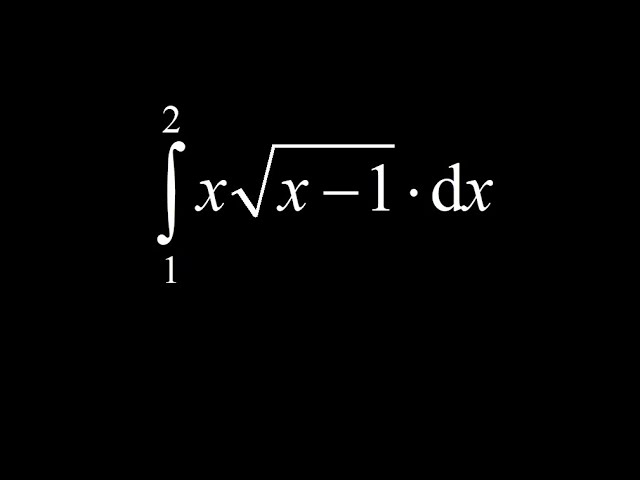
Показать описание
We use a u-substitution and transform the limits of integration to find the definite integral of x*sqrt(x-1) on the interval [1,2].
The standard thing we try first for an integral of this type is to let u equal the interior of the square root. So, we let u=x-1 and du=dx, but we have to take care of the x in the integrand. This is where we solve for x in our original substitution to get x=u+1, and then we can transform the entire integral in terms of u.
Next, we transform the limits of integration to u-space. So we look at the lower bound for x, that's x=1, and we plug into our substitution to find that u=0. Similarly, we plug in the upper limit of x=2 and find that u=1.
Now the entire integral is transformed to u-space and we compute the integral using the power rule and evaluating across the limits of integration.
The standard thing we try first for an integral of this type is to let u equal the interior of the square root. So, we let u=x-1 and du=dx, but we have to take care of the x in the integrand. This is where we solve for x in our original substitution to get x=u+1, and then we can transform the entire integral in terms of u.
Next, we transform the limits of integration to u-space. So we look at the lower bound for x, that's x=1, and we plug into our substitution to find that u=0. Similarly, we plug in the upper limit of x=2 and find that u=1.
Now the entire integral is transformed to u-space and we compute the integral using the power rule and evaluating across the limits of integration.
Definite Integral
Calculus - Definite Integrals
Definite Integral with Absolute Value |2x - 7| from 0 to 7/2
Properties of Integrals and Evaluating Definite Integrals
Calculus - Evaluating a definite integral
Finding definite integrals using area formulas | AP Calculus AB | Khan Academy
Definite integral of piecewise function | AP Calculus AB | Khan Academy
How to Find a Definite Integral using Riemann Sums and the Limit Definition: Quadratic Example
Definite integral jee mains & advanced !! advanced integration !! #definiteintegration
Ex: Definite Integration of an Absolute Value Function Using Geometric Formula
Definite integral of trig function | AP Calculus AB | Khan Academy
Evaluating Definite Integrals Using Geometry
Ex: Evaluate a Definite Integral Using a Geometric Formula (Semicircle)
Definite Integration Basics...How to Integrate ???
DEFINITE INTEGRAL
Finding The Area Under The Curve Using Definite Integrals - Calculus
Learn how to evaluate the definite integral of absolute value by graphing
Indefinite Integral
U-substitution With Definite Integrals
Ex: Evaluate a Definite Integral of a Polynomial
Definite Integral of Piecewise Function
How to evaluate the definite integral with absolute value
Killer Tricks and Shortcuts | Definite Integration | Bhoomika Ma'am | BYJU'S
Ex: Evaluate a Basic Definite Integral of a Basic Quadratic Function Using the FTC
Комментарии
 0:11:05
0:11:05
 0:07:15
0:07:15
 0:04:44
0:04:44
 0:09:48
0:09:48
 0:06:36
0:06:36
 0:04:17
0:04:17
 0:06:13
0:06:13
 0:13:18
0:13:18
 2:01:46
2:01:46
 0:04:21
0:04:21
 0:04:59
0:04:59
 0:17:29
0:17:29
 0:03:14
0:03:14
 0:04:30
0:04:30
 0:20:19
0:20:19
 0:34:24
0:34:24
 0:02:22
0:02:22
 0:10:47
0:10:47
 0:11:03
0:11:03
 0:03:55
0:03:55
 0:04:17
0:04:17
 0:04:33
0:04:33
 0:01:00
0:01:00
 0:02:36
0:02:36