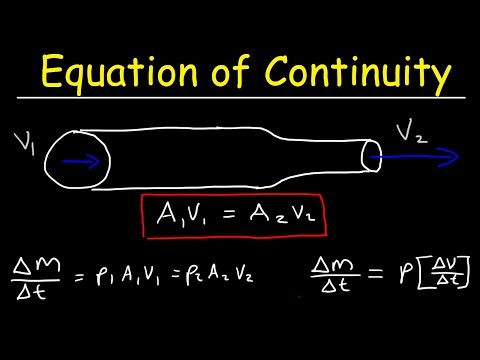
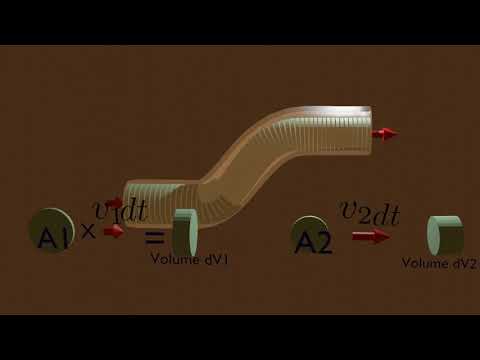
Derivation of the Mass Continuity Equation

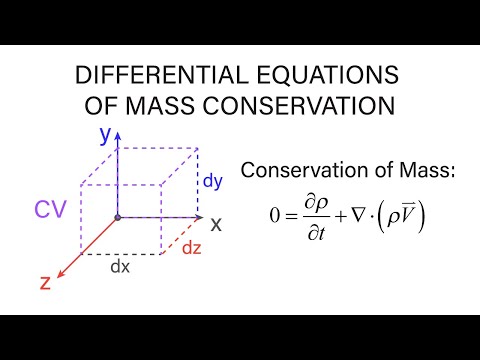
In this video, we will derive the mass continuity equation by having a look at a simple Control Volume (CV). This derivation will then be used for a subsequent video to derive the Navier-Stokes Equations. Animations from Grant Sanderson (aka. 3Blue1Brown) are included.

ONLINE PRESENCE
================

SUPPORT MY WORK
=================

RECOMMENDATIONS
==================

🎵 Cinematic Drama - Epic Royalty Free Background Music

––––––––––––––––––––––––––––––

Contact:

#NavierStokes
#MassConservation
#Mathematics

Time Stamps
----------------------
0:00 - 1:11 : Intro
1:12 - 3:32 : Reynold's Transport Theorem
3:33 - 4:25 : Differential Form
4:26 - 4:55 : Fundamental Equations of Fluid Mechanics
4:56 - 5:19 : Conservation of Mass
5:20 - 6:00 : Momentum Equation
6:01 - 6:08 : Recap Terminology
6:09 - 6:20 : Control Volume (CV)
6:21 - 6:33 : Conservation of Mass (in words)
6:34 - 10:55 : Derivation of the Mass Continuity Equation
10:56 - 14:58 : Explanation of the Divergence
14:59 - End : Outro

[math.physics]

This equation serves as a foundation for many other important concepts in fluid dynamics, and it's intriguing to consider the potential applications of this knowledge in industries such as aerospace, automotive, and power generation. The video not only provides a deeper understanding of the subject matter but also makes one appreciate the elegance and simplicity of the mathematical formulas that govern the natural world.
As a mechanical engineer who has always been passionate about math and physics, I have always been intrigued by the math of fluid mechanics, and also by modern physics, despite neither relativity nor quantum mechanics were part of any course syllabus at my university. I studied these subjects on the side and found them really inspiring, I would go as far as to say that they gave me a novel perspective on life itself. That prompted me to create some online courses on Quantum Mechanics, Quantum Field Theory, special and General Relativity. It’s not my job of course, but I love talking about these topics and showing the "intution" behind the mathematics.

[sangeethsylus]

I have seen so many videos to understand CFD basics but didn't got the point.You explained it simply.Mainly the divergence and convergence point..Nice example.
Make more videos.GOD BLESS YOU BRO.

[manueljenkin]

I'm an Electrical engineer, but I have lots of fascination towards fluid dynamics (and non linearity modelling in general). Thanks a lot for taking your time and effort to make these videos.

[sams.]

This is like a drug for me. I recently shifted from an engineering centric career to corporate strategy consulting. I need more of this in my life!

[deepaksharma]

What the heck.... I never thought my maths 3 is filled up with the equations of fluids nse, gauss & Stokes... Man 👨 u are really clearing up my fogs of my btech.

A loads of thanks brother... Keep un going.. It's really making a huge difference. ☺☺

[abubakarkhartum]

Your explanation on the continuity equation is deep, convincing, and free of ambiguity. Thank you for this piece. Wish you could share me the video to the derivation of the energy equation. This is what the conventional mode of knowledge transfer lacked; visualization of the equations in real life is the key to understanding the physics of any equation and that's what you have been able to bring to the table. Thank once again.

[bwowekeith]

Thanks a lot for the great explanation, and especially the intuitive example for divergence 😊

[ReasonableSwampMonster]

I have used this explanation to help for my graduation project, thank you!

[motapothulasneha]

Thanks!❤
Your effort to make this video is just speechless..
BTW your voice is 🫰

[KhoderAlshaar]

Bro !!! this explanation is just perfect and amazing Plz continue .... lots of love and respect <3 <3 <3 <3

[kudzaimuganhu]

Thank you very much man for the clarified explanations. I am a chemical Eng student n to be honest, you just made my life much easier. Thax a lot.

[michaelchantonese]

wth....it makes sense! Such a good explanation mate. Keep up the good work.

[lupocci]

Great presentation, I really liked it. Just one note: the slide in which you introduce the incompressible fluid equation is wrong, you do not need constant density in time and space. Density can vary in time and space and the fluid can still be incompressible. And also the definition of steady state you gave is wrong.

[jorgemercent]

Thank you so much! Would really appreciate it if you could continue doing tutorials of CFD!

[bonganindlovundlonu]

Thank you so much. Made it pretty easy

[gokuls]

Cool video 👌👍 good explanation about divergence. Expecting more videos from you😊

[andrewcarrillo]

In the reynolds transport eqn, what is U? is is the amount of whatever is fluxing through the cross section?

[andrefilipeasilva]

@Jousef Murad What books do you recommend to learn CFD by using the FEM instead of FVM (used by Ansys)?
Thank you and very nice video!!

[SAIKRISHNA-itjv]

I really liked and enjoyed the video and the explanation is very crisp.


I had a doubt from the finishing part, where u mentioned for source, divergence will be positive and vice versa for sink.


for every control surface the area normal vector will be out of the surface and if any vector field is in the direction of normal vector, it is positive otherwise negative. For source as the velocity vector is out of the control surface (in the direction of normal vector its positive) and for sink velocity is coming towards the center, I mean its opposite to normal vector. so its negative.


bro, is this explanation is
If not let me know the correct


thanks for the informative

[rohitsuryawanshi]

It's a really great video 🤯🎉 thank you ✌