filmov
tv
Derivation of the Continuity Equation
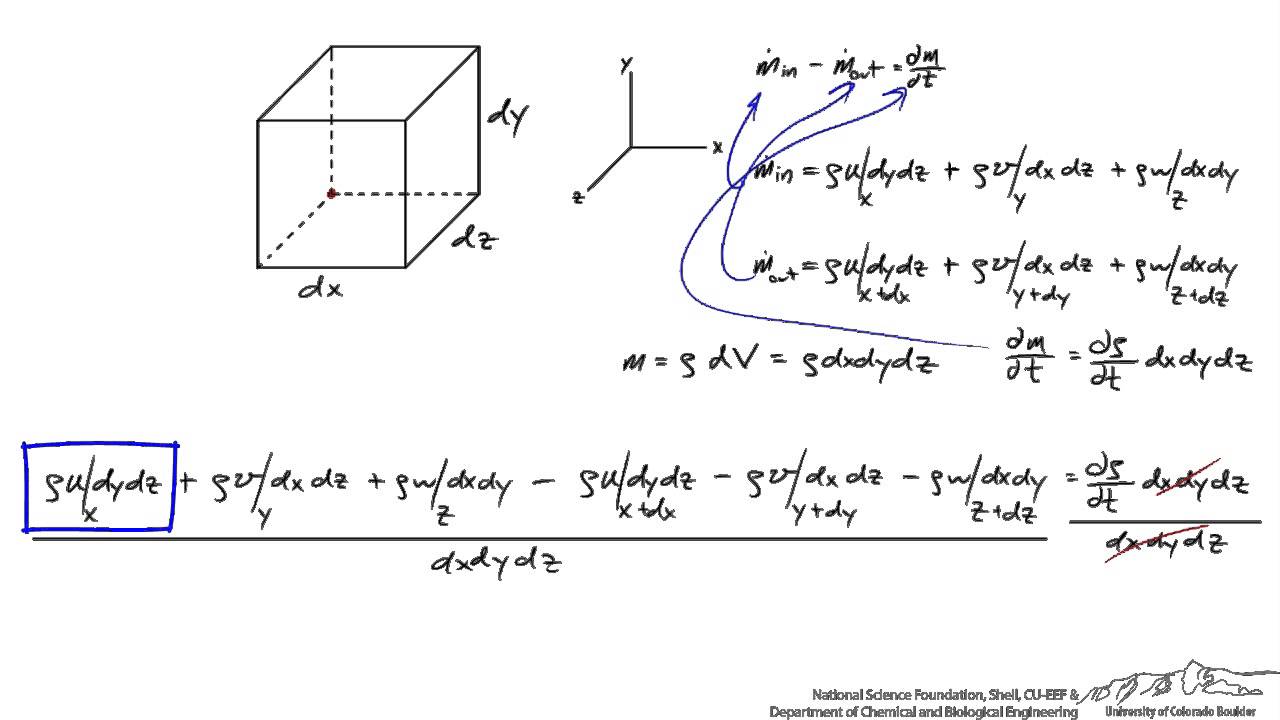
Показать описание
Derives the continuity equation for a rectangular control volume. Made by faculty at the University of Colorado Boulder, Department of Chemical and Biological Engineering.
Check out the Fluid Mechanics playlist here:
Check out the Fluid Mechanics playlist here:
The Continuity Equation (Fluid Mechanics - Lesson 6)
Derivation of the Continuity Equation for Fluid Flow
Derivation of the Continuity Equation
Derivation of the Mass Continuity Equation
Derivation of the continuity equation of fluid dynamics | Lecture 49 | Vector Calculus for Engineers
Electro Magnetics Theory - Continuity of Current
The Continuity Equation: A PDE for Mass Conservation, from Gauss's Divergence Theorem
Understanding Continuity Equation
11th Maths 2 | Chapter 8 | Continuity | Exercise 8.1 | Lecture 2 | Maharashtra Board |
Continuity Equation, Volume Flow Rate & Mass Flow Rate Physics Problems
Continuity Equation Moving fluids and traffic
How Stuff Flows: Continuity Equation Explained for Beginners - Physics + Fluid Mechanics Made Easy
Derivation of 3-D Continuity Equation | FMHM | 3141906 | 2130602 | GTU
Continuity Equation - Explanation, Derivation, Application and Numerical | Fluid Mechanics
continuity equation in 3 dimensions
Equation of Continuity Class 11 Physics Derivation || Mechanical Properties of Fluids Term 2
continuity equation derivation
Continuity Equation - Differential Form
Description and Derivation of the Navier-Stokes Equations
Continuity Equation Semiconductor Derivation Part 1
Flow Rate and Continuity Equation
Deriving The Continuity Equation in Differential form #1 (Conservation of mass)
Continuity of Current: Theory and Derivation Explained
Derive Continuity equation from Maxwell equation
Комментарии
 0:06:04
0:06:04
 0:18:36
0:18:36
 0:06:46
0:06:46
 0:15:45
0:15:45
 0:09:27
0:09:27
 0:02:48
0:02:48
 0:19:01
0:19:01
 0:03:51
0:03:51
 0:43:27
0:43:27
 0:14:01
0:14:01
 0:08:09
0:08:09
 0:08:44
0:08:44
 0:13:13
0:13:13
 0:20:49
0:20:49
 0:13:06
0:13:06
 0:05:48
0:05:48
 0:06:03
0:06:03
 0:24:17
0:24:17
 0:11:18
0:11:18
 0:10:23
0:10:23
 0:03:49
0:03:49
 0:05:03
0:05:03
 0:10:51
0:10:51
 0:02:20
0:02:20