QIP2021 | Quantum Copy-Protection... // Secure Software Leasing... (Poremba&Lord)

Quantum Copy-Protection of Compute-and-Compare Programs in the Quantum Random Oracle Model // Secure Software Leasing Without Assumptions

Authors: Andrea Coladangelo, Christian Majenz and Alexander Poremba // Anne Broadbent, Stacey Jeffery, Sébastien Lord, Supartha Podder and Aarthi Sundaram

Affiliations: UC Berkeley | CWI and QuSoft | Caltech // University of Ottawa | QuSoft and CWI | University of Ottawa | University of Ottawa | Microsoft Quantum

Abstract
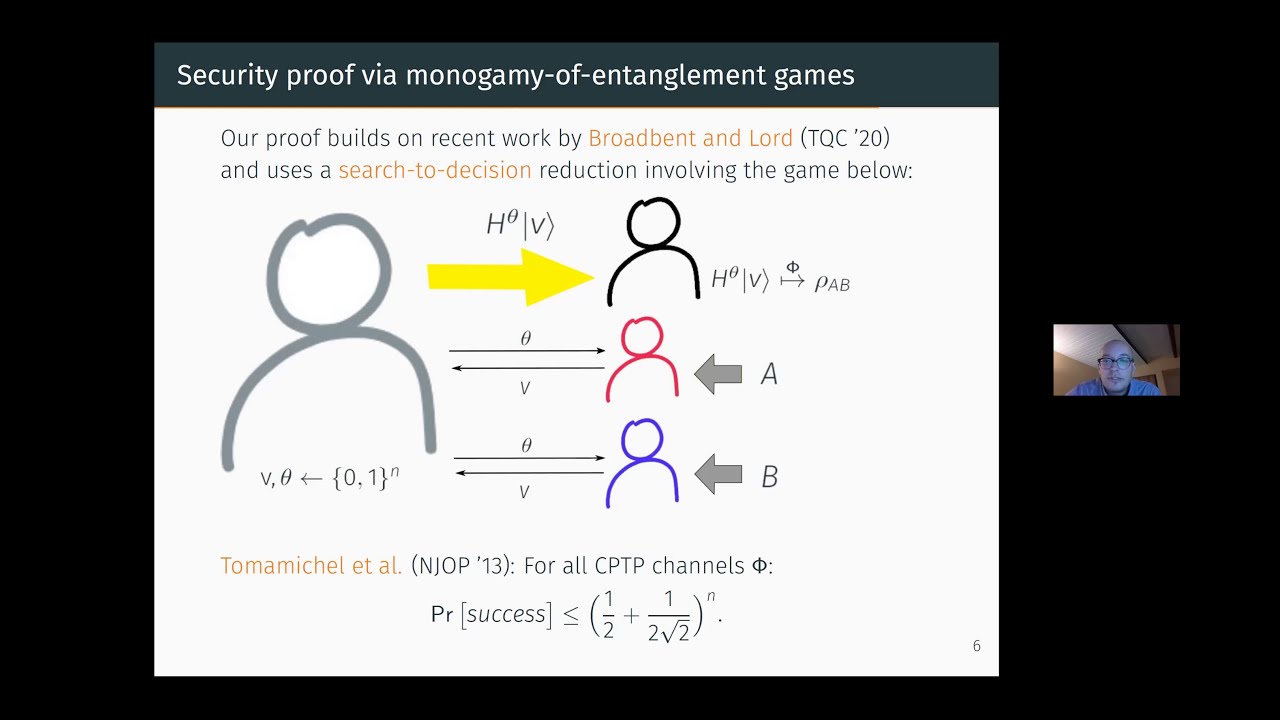
Copy-protection allows a software distributor to encode a program in such a way that it can be evaluated on any input, yet it cannot be ``pirated'' -- a notion that is impossible to achieve in a classical setting. Aaronson (CCC 2009) initiated the formal study of quantum copy-protection schemes, and speculated that quantum cryptography could offer a solution to the problem thanks to the quantum no-cloning theorem. In this work, we introduce a quantum copy-protection scheme for a large class of evasive functions known as ``compute-and-compare programs'' -- a more expressive generalization of point functions. A compute-and-compare program CC[f,y] is specified by a function f and a string y within its range: on input x, CC[f,y] outputs 1, if f(x) = y, and 0 otherwise. We prove that our scheme achieves non-trivial security against fully malicious adversaries in the quantum random oracle model (QROM), which makes it the first copy-protection scheme to enjoy any level of provable security in a standard cryptographic model. As a complementary result, we show that the same scheme fulfils a weaker notion of software protection, called ``secure software leasing'', introduced very recently by Ananth and La Placa (eprint 2020), with a standard security bound in the QROM, i.e. guaranteeing negligible adversarial advantage. // Quantum cryptography is known for enabling functionalities that are unattainable using classical information alone. Recently, Secure Software Leasing (SSL) has emerged as one of these areas of interest. Given a target circuit C from a circuit class, SSL produces an encoding of C which enables the evaluation of C, and also enables a verify procedure, by which the originator of the software becomes convinced that the software is returned --- meaning that the recipient has relinquished the possibility of any further use of the software. Clearly, such functionality is unachievable using classical information alone, since it is impossible to prevent a user from keeping a copy of the software. Recent results have shown the achievability of SSL using quantum information for a class of functions called compute-and-compare (these are a generalization of the well-known point functions). These prior works, however, all make use of setup or computational assumptions. Here, we show that SSL is achievable for compute-and-compare circuits without any assumptions. Our technique is a generic reduction from any quantum message authentication code to such an SSL scheme. Along the way, we also show that point functions can be copy-protected without any assumptions, for a security definition that involves one honest and one malicious evaluator.

Get entangled with us!