retrocausal nonlocal noncommutative photon quantum weirdness Valentina Parigi & John G. Cramer

My own take on a quantum weirdness noncommutative photon experiment!!
Ruth E. Kastner, Ph.D. on quantum physics, transactional model
"Basically RTI agrees with this in the sense that metrical time
(the 'time' of 'spacetime') is generated by transactions, which
always involve the 'choice' of a particular observable, so that there
is a commutative space for the emission and absorption events. But
this is physically real--it really happens-- it's not a matter of our
ignorance. Metrical time is really physically generated. So when we
perceive the passage of time in this way, it's not illusory. It's
veridical. Only the measure of 'how much time has passed' is relative
to our inertial frame--our internal clock at the quantum level, which
is also physically real and based on the intrinsic periodicity of
fermionic spin. The latter however is not a spacetime process. See
Chapter 8 of my 2nd edition, excerpted material here:
" It is reasonable to think that there are also two ways to define WF [Wigner Function] in the deformation quantization of NCQM. [noncommutative quantum mechanics] In the NCQM case, Eq. (2) has
been extended to Eq. (6) to reflect the characteristic of noncommutative space. Correspondingly, as in this work we
demonstrated, Eq. (1) should also be replaced by Eq. (12) to give the WF of NCQM. Once having solutions of the effective Schrödinger equation (3) of NCQM, one can obtain the related WF by Eq. (12)."
A new form of Wigner functions on the noncommutative space ✩
Sicong Jing ∗, Taihua Heng, Fen Zuo
There are very compelling, and in my opinion enlightening reasons to call the Weyl transform a noncommutative Fourier transform.
Quantum theories can be naturally interpreted as noncommutative probability theories. The observables are noncommutative random variables, and states are noncommutative probabilities.
The Weyl observables are unitary, and therefore noncommutative phases. In fact, they exactly play the role of noncommutative characters.
Regardless, the Weyl–Wigner transform is a well-defined integral transform between the phase-space and operator representations, and yields insight into the workings of quantum mechanics. Most importantly, the Wigner quasi-probability distribution is the Wigner transform of the quantum density matrix, and, conversely, the density matrix is the Weyl transform of the Wigner function.
the latter two are unaffected by the non-commutative parameter θ, however,
both the butterfly and entanglement velocities increase with the strength of the non-commutativity. This implies that non-local interactions can enhance the effective light-cone for the transfer of quantum information, eluding previously conjectured bounds encountered in the context of local quantum field theory. We comment on a possible limitation on the retrieval of quantum information imposed by non-locality.
. With this holographic definition, it has been shown that for small enough regions the entanglement entropy follows instead
a volume law, while for large regions the standard area law (2.11) is recovered [88, 89]. This transition from a volume law to an area law behaviour has also been observed in quantum field theory calculations [90–92] and has been understood as a result of the non-
locality inherent of non-commutative theories [93, 94]
In this paper it was found that the entanglement velocity vE is
generically larger that the commutative counterpart, even exceeding the speed of light in the limit of very strong non-commutativity."
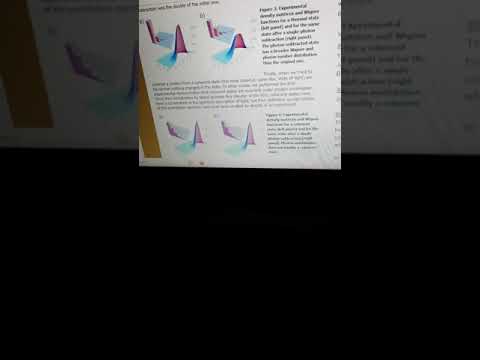
"We formulate an analytical expression of the Wigner function after the subtraction or addition of a single photon, for arbitrarily many modes. It is used to demonstrate entanglement properties specific to non-Gaussian states and also leads to a practical and elegant condition for Wigner function negativity. "
Entanglement and Wigner Function Negativity of Multimode Non-Gaussian States
Mattia Walschaers, Claude Fabre, Valentina Parigi, and Nicolas Treps
Phys. Rev. Lett. 119, 183601 – Published 31 October 2017
For mixed initial states, it is unclear that
subtraction or addition in a mode which is not part of such a
mode basis automatically leads to inherent entanglement,
because also convex decompositions which are not of the
form (12) must be considered.

[voidisyinyangvoidisyinyang]

Ruth E. Kastner
3:03 PM (1 minute ago)
to me
Yes. One can think of matter (fermionic stuff) as 'trapped light'. Or
"hidden light".

[voidisyinyangvoidisyinyang]

In Fig. 2, we subtract a single photon from a
supermode, which leads to negativity only if the super-
mode is sufficiently squeezed (this is the case for merely
three modes). Nevertheless, Fig. 3 shows that subtraction
from a coherent superposition of supermodes has an
advantage regarding the state’s negativity. For 54% of the
randomly chosen superpositions, i.e., random choices of
g ∈ N ðR2mÞ, the Wigner function has a negative region.
This underlines the potential of mode-selective photon
subtraction to generate states with both a negative Wigner
function and inherent entanglement.

[voidisyinyangvoidisyinyang]

h-bar is inherently time-frequency uncertainty since it's 1/2 spin as h/2pi. This is why Roger Penrose states since 1996 that gravity is the collapse of quantum nonlocality from h-bar/time-frequency uncertainty. So as John G. Williamson and Fred Alan Wolf both point out - along with Ruth E. Kastner, Ph.D., and Gerard 't Hooft with Martin van der Mark - the electron originates from a "moebius strip" of light as the 720 degrees (to measure the position of the electron). The 1/2 spin is inherent nonlocality of the light that then "collapses" into the 720 degree as the noncommutative "measurement" of external reality, thereby creating gravity (and also perceptual awareness as linear causality of spacetime).
You can think of Planck's Constant as the "average energy of light" but it is inherently noncommutative from time-frequency noncommutativity. Planck "canceled out" this noncommutativity when he converted it to joules by assuming a symmetric spatial measurement.
Ruth E. Kastner
3:03 PM (1 minute ago)
to me
Yes. One can think of matter (fermionic stuff) as 'trapped light'. Or
"hidden light".
John G. Williamson: "Another major mystery of physics is how fermions may arise from bosons and just what the fundamental underlying nature of fermions and bosons is anyway. Consider the spin of the double-looped object. Given the momentum of the constituent photon, it is straightforwards to calculate the spin of the photon momentum in the double looped object. This is just the characteristic length scale of the model λC/4π times the initial photon momentum hc/λC . That is the numerical value is half integral: h-bar/2 . The total spin is then, by symmetry also half-integral since that of the initial photon rotates, averaging out to zero. By the spin-statistics theorem, therefore, the proposed object is a fermion. More fundamentally, as is clear from figure 3, the object is double-covering over the torus in momentum space and returns to its starting configuration after a 720-degree rotation in the space of an outside observer."
So there is a "hypertube" to light as J.P. Vigier emphasized from Louis de Broglie.
Fred Alan Wolf (who co-authored Beyond SpaceTime with Jack Sarfatti)
"The universe of matter is made by mixing together various kinds of light. Actually there’s only two basic kinds. One we call spin-½, and the other we call spin-1. The spin-1 kind of light doesn’t interact very well with the mind-of-God [Higgs] field. Once it’s released, it’s allowed to do its thing: it carries information, it becomes the medium by which we become aware of what’s going on. And it interacts with the spin-½ kind of light, which is zigzagging in the mind of God. So the mind of God is constantly buttressing and playing with the spin-½ kind of light. And the spin-½ kind of light then sends messages backward and forward using the spin-1 kind of light. These notions of spin-½ and spin-1 have to do with another kind of name. When light’s behaving that way, [when it’s behaving as] spin-½, we call them fermions, and when it’s spin-1 we call them photons, or ordinary light. So these are just more nomenclature, but you don’t have to know all that. Basically that’s how it works. Everything is made of light, and once one understands that, then one uses light as the medium by which the message is composed."

[voidisyinyangvoidisyinyang]

Particularly relevant to current experimental progress is our conclusion that subtraction from a superposition of supermodes can produce inherently
entangled states with nonpositive Wigner functions, thus
paving the road to quantum supremacy applications."
Entanglement and Wigner Function Negativity of Multimode Non-Gaussian States
Mattia Walschaers, * Claude Fabre, Valentina Parigi, and Nicolas Treps
Laboratoire Kastler Brossel, UPMC-Sorbonne Universités, ENS-PSL Research University,
Collège de France, CNRS; 4 place Jussieu, F-75252 Paris, France
(Received 10 July 2017; published 31 October 2017)

[voidisyinyangvoidisyinyang]

Entanglement and Wigner Function Negativity of Multimode Non-Gaussian States Mattia Walschaers, Claude Fabre, Valentina Parigi, and Nicolas Treps

[voidisyinyangvoidisyinyang]

Within the new theory a new kind of solution, equation (5) has been proposed
satisfying the (field only) Maxwell equations. This solution has energy proportional to frequency, a fixed angular
momentum limit and is identified with the physical photon. Extending the Maxwell equations by introducing a
further rest-mass component has allowed qualitatively new kinds of solutions containing, as well as the rest-mass
component, re-circulating field components. Such solutions are necessarily charged, have half-integral spin and
have the proper 720 degree symmetry of fermions. These act as a possible centre for the emission and absorption
of photons. These solutions are identified with the electron and positron. Possible routes for the experimental

[voidisyinyangvoidisyinyang]

What do you think of John G. Williamson's claim that the electron is actually a photon?
Another major mystery of physics is how fermions may arise from bosons and just what the fundamental underlying nature of fermions and bosons is anyway. Consider the spin of the double-looped object. Given the momentum of the constituent photon, it is straightforwards to calculate the spin of the photon momentum in the double looped object.14 This is just the characteristic length scale of the model λC/4π times the initial photon momentum hc/λC . That is the numerical value is half integral: h-bar/2 . The total spin is then, by symmetry also half-integral since that of the initial photon rotates, averaging out to zero. By the spin-statistics theorem, therefore, the proposed object is a fermion. More fundamentally, as is clear from figure 3, the object is double-covering over the torus in momentum space and returns to its starting configuration after a 720-degree rotation in the space of an outside observer.
Isn't this really what Fred Alan Wolf means when he refers to the 1/2 spin type of light?

[petersvideofile]

Hey thanks as always! Check this video out from 1:10:00 mark ""FESIG 84th Meeting William Alek on Anti-Gravity Field Propulsion 6Jan21" when he talks about bearden and neg energy from reverse propagating em waves in standing waves. This sounds very similar to what you are saying but it is yet another macro analog. You may want to get in touch with this alek guy. :). Honestly man everything you are finding proof in peer reviewed journals relating to this stuff has proof for macro analogs with larger coherent quantum fields I think :)