filmov
tv
Parallel Axis Theorem Derivation

Показать описание
Next Video: Parallel Axis Theorem Example
Previous Video: Uniform Solid Cylinder Moment of Inertia Derivation
Content Times:
0:00 The Parallel Axis Theorem
0:44 The Derivation Setup
2:32 Organizing the Integral(s)
5:49 Taking the Integral(s)
8:25 The Parallel Axis Theorem
#RotationalInertia #MomentOfInertia #ParallelAxisTheorem
29.6 Deep Dive - Derivation of the Parallel Axis Theorem
29.4 Parallel Axis Theorem
Parallel Axis Theorem Derivation
Proof of the Parallel Axis Theorem
Proof of Parallel Axis Theorem
Parallel Axis Theorem & Moment of Inertia - Physics Practice Problems
Engineering Mechanics: Statics Theory | Parallel Axis Theorem
Parallel|Axis|Theorem|Physics 11|Tamil|MurugaMP
Parallel Axis Theorem | Statement & Derivation | HSC 12th | Physics | Science
How to apply Parallel axis theorem
Parallel Axis Theorm- Lec# 5|| Mechanics For BS and BSc
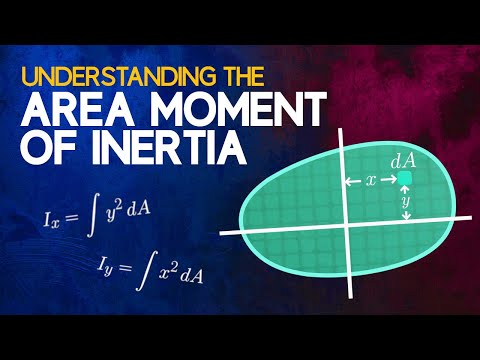
Understanding the Area Moment of Inertia
Parallel Axis Theorem🔥 | Statement, Proof | Moment Of Inertia | Engineering Mechanics | Civil Stuff...
12th Rotational Dynamics l Parallel Axis Theorem l Sahyadri Tutorials
Parallel axes theorem proof | Rotational motion | moment of inertia
The Parallel Axis Theorem (Steiner's Theorem) | Classical Mechanics
Parallel axis theorem | Mechanics | lecture 7 | BSc | BS physics | AdS | physics ka safar
Parallel Axis Theorem Derivation
Parallel Axis Theorem
Statics: Lesson 68 - Parallel Axis Theorem, Area Moment of Inertia
12th Physics | Chapter No 1 | Rotational Dynamics | Lecture 8| JR Tutorials |
Proof of Parallel Axis Theorem. Moment of inertia ( Mechanics ) By: Muhammad Anas Amjad
Plus One Model Exam | Physics | Parallel Axis Theorem | Exam Winner
parallel axis theorem| rotational dynamics JEE NEET BOARDS #exam #viral #learning @GyanFreedom
Комментарии
 0:05:38
0:05:38
 0:04:11
0:04:11
 0:09:15
0:09:15
 0:04:05
0:04:05
 0:07:19
0:07:19
 0:11:34
0:11:34
 0:11:58
0:11:58
 0:10:19
0:10:19
 0:14:54
0:14:54
 0:03:34
0:03:34
 0:15:49
0:15:49
 0:11:05
0:11:05
 0:11:58
0:11:58
 0:11:52
0:11:52
 0:10:22
0:10:22
 0:02:32
0:02:32
 0:20:18
0:20:18
 0:15:05
0:15:05
 0:03:34
0:03:34
 0:14:21
0:14:21
 0:17:59
0:17:59
 0:11:05
0:11:05
 0:12:09
0:12:09
 0:00:24
0:00:24