filmov
tv
Moment Generating Function - Part 1

Показать описание
In this video we defined MGF and derived MGF of Exponential, Uniform and Bernoulli distributions to find their expectation and variances.
Thank you
What is a Moment Generating Function (MGF)? ('Best explanation on YouTube')
Moment Generating Functions (Part 1)
Moment Generating Function - Part 1
Moment generating functions -- Example 1
Properties of Moment Generating Functions: An Example.
Moment Generating Function - Part 2
Lesson 15: Moment Generating Functions
MA 381: Section 11.1: Moment Generating Functions, Part 4
MA 381: Section 11.1: Moment Generating Functions, Part 3
Moment Generating Function Part 3
Moment Generating Functions (Part 2)
Moment generating functions -- Example 2
Moment Generating Functions (Part 8)
Moment Generating Function of the Binomial Distribution
Math Stats L02a Part 2 Using moment generating functions (mgfs) to find limiting distributions
Using Moment Generating Functions to find the Variance: Example 1
Moment Generating Function of a Gaussian
Math Stats L02a Part 3 Using moment generating functions (mgfs) to find limiting distributions
Probability Theory L47b Section 5.4 Part 2 Moment Generating Function Technique for Transformations
Moment Generating Function for Discrete Random variables
Normal distribution moment generating function
Moment Generating Function (MGF) of Exponential Distribution (Part 4)
Module 15 Moment Generating Function Part 2 153EI75f9PQ
Moment Generating Functions|| Part 2 || in English
Комментарии
 0:08:51
0:08:51
 0:08:25
0:08:25
 0:05:19
0:05:19
 0:04:39
0:04:39
 0:07:23
0:07:23
 0:16:53
0:16:53
 0:08:54
0:08:54
 0:06:43
0:06:43
 0:09:11
0:09:11
 0:04:54
0:04:54
 0:04:38
0:04:38
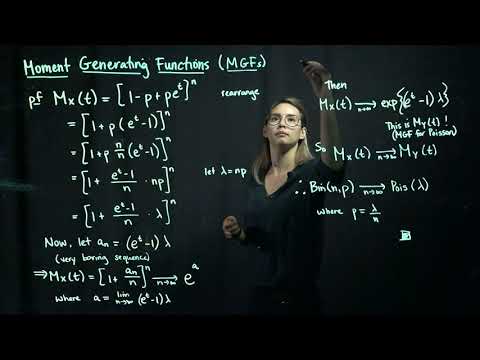 0:03:50
0:03:50
 0:26:06
0:26:06
 0:17:31
0:17:31
 0:04:52
0:04:52
 0:05:44
0:05:44
 0:14:37
0:14:37
 0:18:06
0:18:06
 0:25:45
0:25:45
 0:02:43
0:02:43
 0:14:49
0:14:49
 0:17:23
0:17:23
 0:09:41
0:09:41