Mean Value Theorem For Integrals

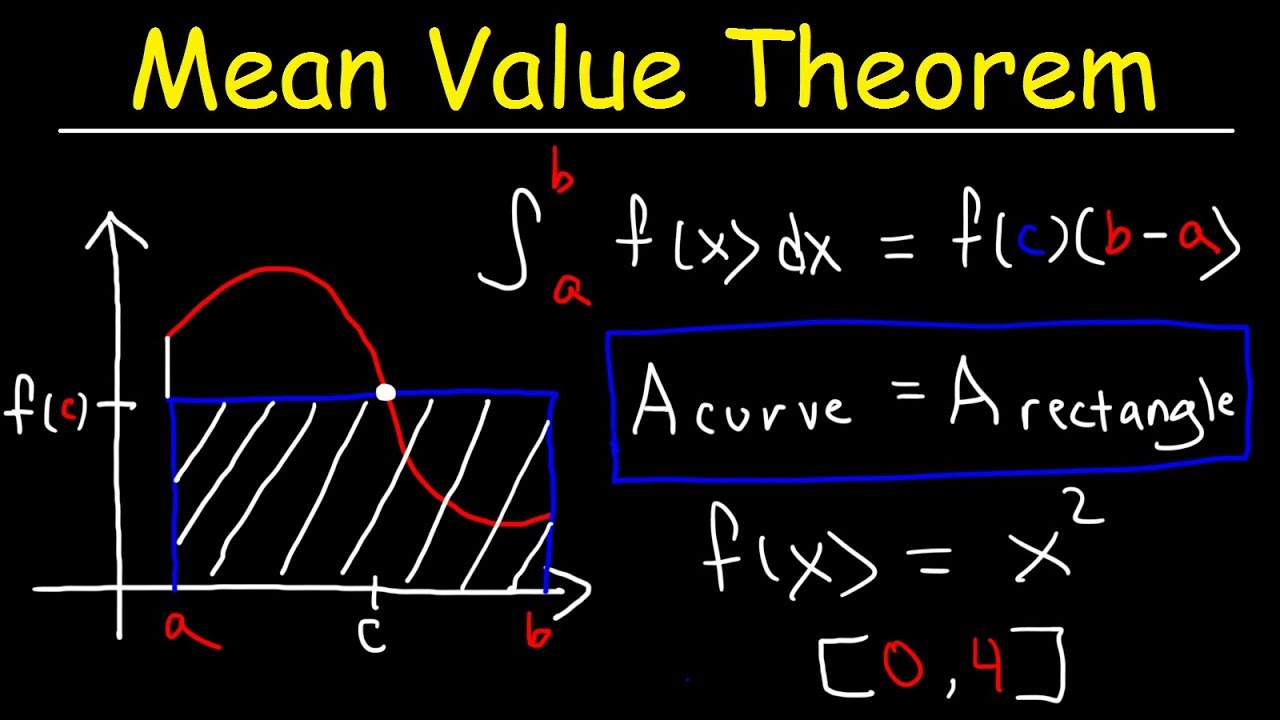
This calculus video tutorial provides a basic introduction into the mean value theorem for integrals. It explains how to find the value of c in the closed interval [a, b] guaranteed by the mean value theorem where the area under the curve is equal to the area of the rectangle at x = c. This video contains plenty of examples and practice problems. You need to be familiar with the process of finding antiderivatives and evaluating definite integrals.

Antiderivatives:

Fundamental Theorem - Part 1:

Fundamental Theorem - Part 2:

Net Change Theorem:

Mean Value Theorem - Integrals:

________________________________
Average Value of a Function:

U-Substitution - Indefinite Integrals:

U-Substitution - Definite Integrals:

1st Order Differential Equations:

Initial Value Problem:

________________________________
Area Between Two Curves:

Disk and Washer Method:

Volume By The Shell Method:

Volume By Cross Sections:

Arc Length Calculus Problems:

__________________________________
Calculus Final Exam and Video Playlists:

Full-Length Videos and Worksheets:

[wewillmakeyouaplaceforthew]

man this guy took just 1 minute to get through my thick skull for this very concept my AP teacher took a long anxiety inducing, painful mind bending lecture.

this teach is an artist, truly skilled in his works.

[tatyana]

You stay saving my grade man. Your videos are the best. You've helped me through so many classes.

[everodarte]

Never stop please I have been watching you since highschool and you have saved me so many times

[joodimourhli]

Amazing! I have a test with this material on Sunday, and this helped me a lot! Thank youu

[yazansalama]

You are the best teacher in the world. Thank you so much.

[georgesadler]

Professor Organic Chemistry Tutor, thank you for explaining the Mean Value Theorem for Integrals with graphs and examples from start to finish. This is an error free video/lecture on YouTube TV with the Organic Chemistry Tutor.

[mattmiller]

Learned this and understood it decently, but teacher chose to have the formula as (∫f(x)dx from x=a to b)/(b-a)=f(c). I suppose it's the same thing, not sure if easier or the same difficulty. Also our first in-class practice problem was much more difficult: ∫sinx(e^cosx)dx from x=0 to (pi/2). That didn't make understanding it any easier. Thanks for the video, helped clarify some questions.

[safianaseer]

very well explained.... salute to you sir

[world]

Thanks for all this explains sir
so much 👍

[mohammadsafiedien]

You're better than my teacher at university

[ChefFarisMom]

Thank you much
Kindly teach the second mean value theorem for integrals.

[Dipslox]

remember the second part about 1/(b-a) * integral for the average change of the function

[esthereuticterra]

C represents where the area under the function f(x) is equal to the area of the rectangle over the interval [a, b]

[snowballdrifter]

I'm confused, why did he not use the formula f'c=f(b)-f(a)/b-a ?? Would it have the same final answer?

[viln]

if you play this at 1.5 speed he sounds like Ben Shapiro
1 day before the final ez fail

[watching]

What is this used for in applications (real life) is this to find average position or velocity between a time range?

[vinhquachvlog]

thank you, this helped me a lot for the test

[minahany]

i think u made a mistake in the question where (x)^1/2 [1, 9] answer should be much higher than that

[randolfshemhusain]

There's an easier way to get the value of c, but that involves using the average of the function

[yanhesap]

8:26 Should C has been + or minues 4.694?