filmov
tv
(Abstract Algebra 1) The Division Algorithm

Показать описание
A proof of the division algorithm using the well-ordering principle.
(Abstract Algebra 1) The Division Algorithm
Abstract Algebra | 1. The Division Algorithm
Abstract Algebra | The division algorithm for polynomials.
(Abstract Algebra 1) Divisors
Division Theorem/Division Algorithm
Number Theory: The Division Algorithm
(Abstract Algebra 1) Greatest Common Divisor
Teaching myself abstract algebra
Class 10th A.P imp sums #shorts #shortsfeed #ytshorts #viralshorts #maths #mathsshorts #ncertmaths
Abstract Algebra | Corollaries and examples of the division algorithm for polynomials.
Field Definition (expanded) - Abstract Algebra
Abstract Algebra Section 1.3. The division algorithm
Abstract Algebra: Division Algorithm Proof
Abstract Algebra Lectures Part 19: Division Algorithm in K[t]
Abstract Algebra 15.1: Division Algorithm
Polynomial Rings and Division -- Abstract Algebra 22
Math Book for Complete Beginners
Abstract Algebra Presentation #1 (Polynomial Long Division).
PEMDAS Math Problem | Algebra Fundamentals | JusticeTheTutor #math #shorts #maths #mathstricks
Ring Definition (expanded) - Abstract Algebra
Group Definition (expanded) - Abstract Algebra
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Cyclic Groups (Abstract Algebra)
What is a Group? | Abstract Algebra
Комментарии
 0:16:32
0:16:32
 0:17:57
0:17:57
 0:20:34
0:20:34
 0:05:03
0:05:03
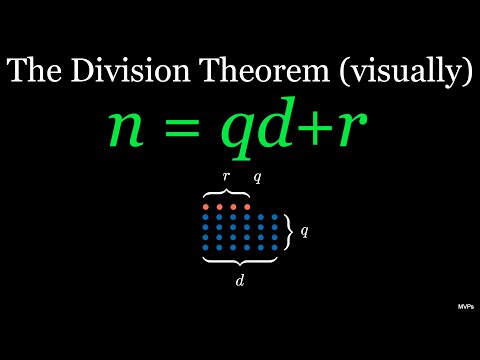 0:02:33
0:02:33
 0:12:49
0:12:49
 0:11:48
0:11:48
 0:14:41
0:14:41
 0:00:34
0:00:34
 0:17:40
0:17:40
 0:08:06
0:08:06
 0:09:04
0:09:04
 0:13:06
0:13:06
 0:27:20
0:27:20
 0:08:48
0:08:48
 0:52:23
0:52:23
 0:00:21
0:00:21
 0:16:23
0:16:23
 0:00:29
0:00:29
 0:06:51
0:06:51
 0:11:15
0:11:15
 0:00:38
0:00:38
 0:05:01
0:05:01
 0:19:46
0:19:46