Prove Algebraically That The Sum Of The Squares Of Any 2 Positive Odd Integers Is Even (Maths Proof)

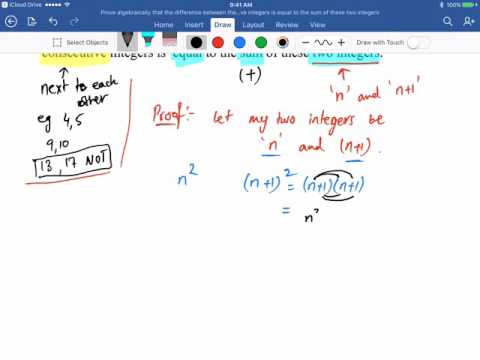
In this video you will need to prove that the sum of the squares of 2 odd integers is always even. To do this call the first integer 2n-1 and the second odd integer 2n+1. Squaring 2n+1 gives 4n^2-4n+1. You get this by multiplying out the double bracket (2n-1)(2n-1). Squaring the second bracket gives 4n^2+4n+1. Since sum means add, add these expressions to give 8n^2+2. Now to prove this answer is a multiple of 2 factorise 8n^2+2 to give 2(4n^2+1).