filmov
tv
Why is 0! equal to 1?

Показать описание
In this video I talk about the definition of factorial and the value of 0! #math #factorial #zero #integral
Why is 0! = 1?
Why do numbers to the power of 0 equal 1?
Why does 'x to the zero power' equal 1?
Prove that Zero Factorial is Equal to One
1 divided by 0 is equal to || One by zero | Division by Zero
But Why Does 0 Factorial Equal 1
Why 0! = 1 ? | Why 0 factorial is equal to 1? #shorts
Teacher explains all why is everything raised to the zero power equal to one
Simplify ((0!−1)/(0!+1))! #fyp #viralvideo #funmaths #maths #math
Why is 0! equal to 1?
why 0/0 is not defined || why 0/0 is not equal to 1 ? || why 0/0 is indeterminate form ?
0 by 0 = 1 | Zero By Zero is Equal To One | 0 / 0 = 1 | PROVED | Maths Rule Fails |
Why 0 factorial is equal to 1
Why Does a Number Raised to Zero Equal One
0!=1 PROOF | Zero Factorial is Equal to One
Can Zero Power Zero Be Equal To 1? 0 Power 0 = 1? Maths Failed Again.
why anything to the power zero is equal to 1?
Proof that 0/0 = 2 | Proof that 0 by 0 equal to 2
Anything into 0 is equal to 0 | BUT WHY ??? | Easy Question | Aman Sir Maths | Bhannat Maths
Why is a number raised to 0 equal to 1?
Zero factorial DOES NOT equal 1 - Explained!
Why does ' a to the zero power' equal 1(a0 =1 )?
any number power 0 equal 1 why? (Urdu/Hindi) lecture
Why is 2 raised to power 0 equal to 1? | Facts in minutes | Monica Bedi
Комментарии
 0:06:05
0:06:05
 0:05:58
0:05:58
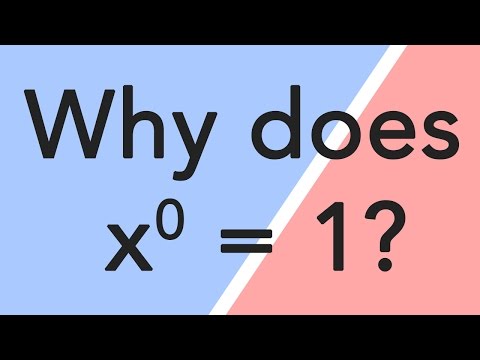 0:02:15
0:02:15
 0:01:58
0:01:58
 0:00:49
0:00:49
 0:04:49
0:04:49
 0:01:00
0:01:00
 0:04:47
0:04:47
 0:00:41
0:00:41
 0:02:17
0:02:17
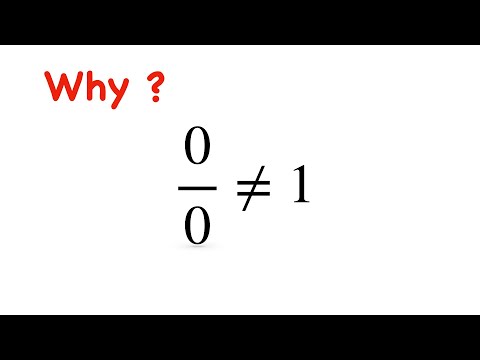 0:02:49
0:02:49
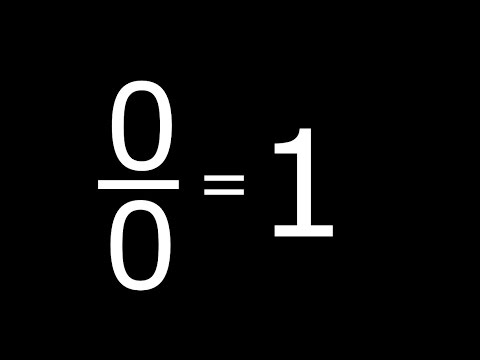 0:01:04
0:01:04
 0:04:51
0:04:51
 0:02:43
0:02:43
 0:03:30
0:03:30
 0:03:02
0:03:02
 0:02:14
0:02:14
 0:02:45
0:02:45
 0:02:55
0:02:55
 0:03:31
0:03:31
 0:06:57
0:06:57
 0:00:52
0:00:52
 0:01:52
0:01:52
 0:03:12
0:03:12