filmov
tv
Identifying f, f', and f'' based on graphs
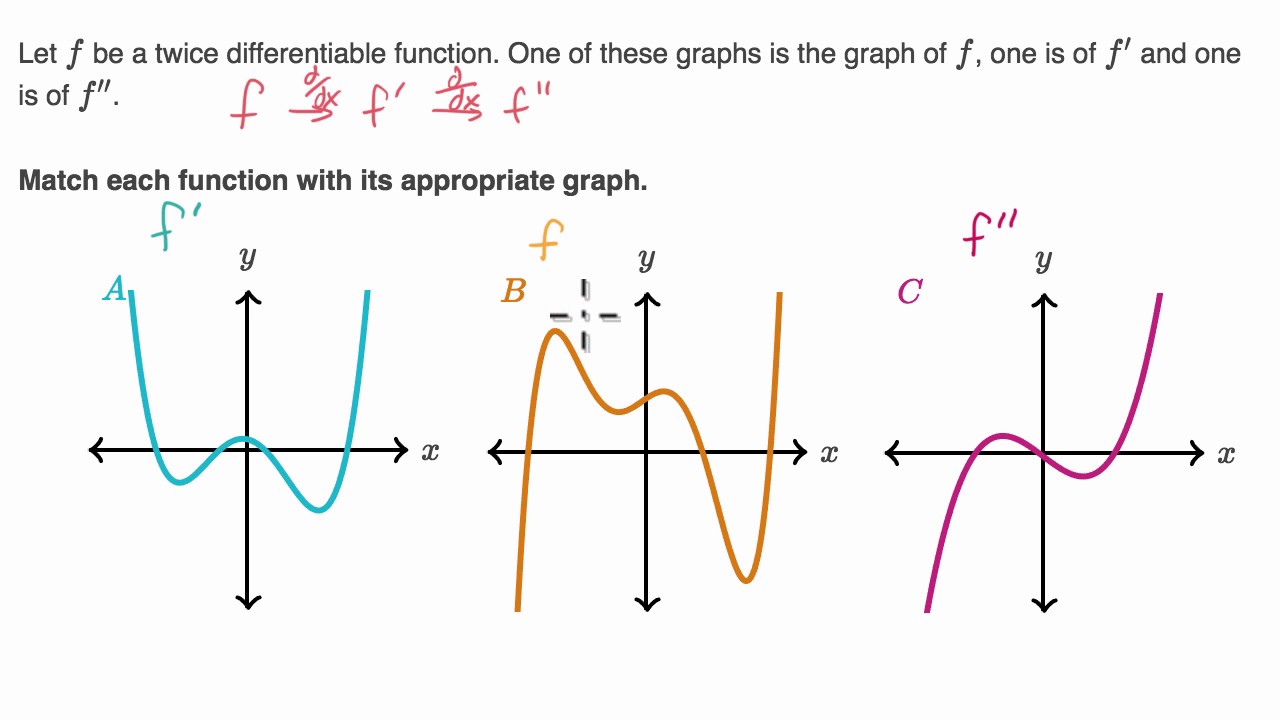
Показать описание
Worked example matching a function, its first derivative and its second derivative to the appropriate graph.
Identifying f, f', and f'' based on graphs
Connecting f, f', and f'' graphically | AP Calculus AB | Khan Academy
Math 1A HW 2.7.41 The figure shows the graphs of f, f ', and f ''. Identify each curv...
Identifying f, f' and f'' From a Graph
Given fx sketch the first and second derivative graph
Points of inflection from the graphs of f, f' or f''
50. The figure shows graphs of f, f', f'', f''''. Identify each c...
Connecting f, f', and f'' graphically (another example) | AP Calculus AB | Khan Acade...
AP Calculus Connecting F, F’, and F’’
Finding derivatives from a graph
Ex: Determine the Sign of f(x), f'(x), and f''(x) Given a Point on a Graph
How to use the graph of f' to identify the intervals on which f is increasing or decreasing
Identifying a function's derivative example | Differential Calculus | Khan Academy
Use a graph of the function to identify f' and f'' intervals
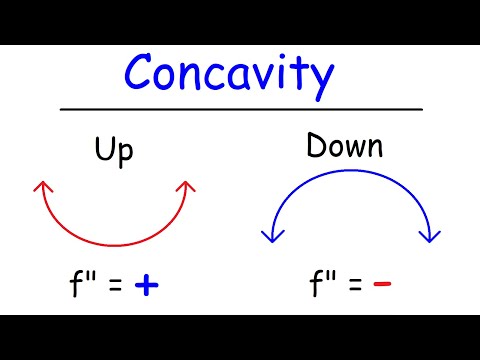
Concavity, Inflection Points, and Second Derivative
Matching Graphs of Functions and Their Derivatives
Sketching a Derivative from the Graph of a Function
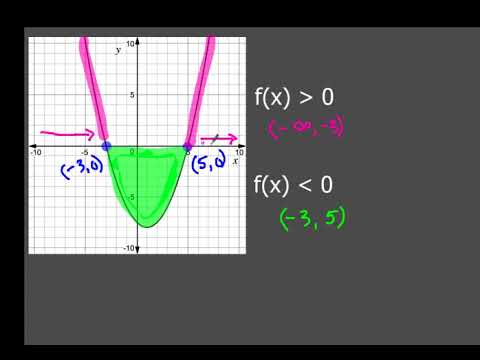
How To Tell Where f(x) is Less Than 0 or Greater Than 0
Identify the Function, Derivative, and 2nd Derivative Given Just the Graphs (2)
(fog)(x) and (gof)(x): How to find them, given f(x) and g(x).
Unit #4 Review... (Sec 4.3) Identify f' and f' from a graph
Given the derivative graph of f' find the relative min
Identifying a Function from its Derivative
Identifying Functions (8.F.1)
Комментарии
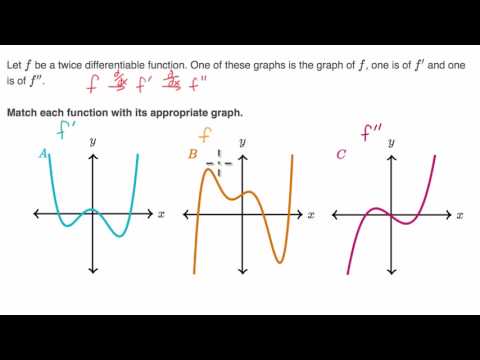 0:04:27
0:04:27
 0:05:36
0:05:36
 0:03:50
0:03:50
 0:04:26
0:04:26
 0:04:09
0:04:09
 0:04:32
0:04:32
 0:02:18
0:02:18
 0:04:21
0:04:21
 0:09:37
0:09:37
 0:05:21
0:05:21
 0:05:30
0:05:30
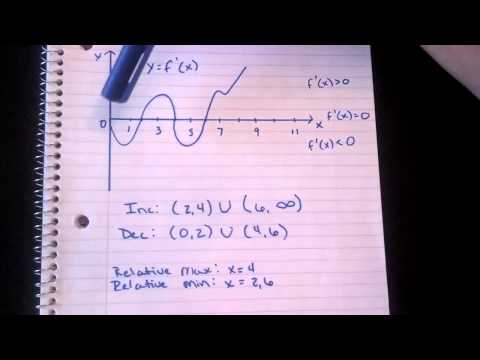 0:01:07
0:01:07
 0:02:37
0:02:37
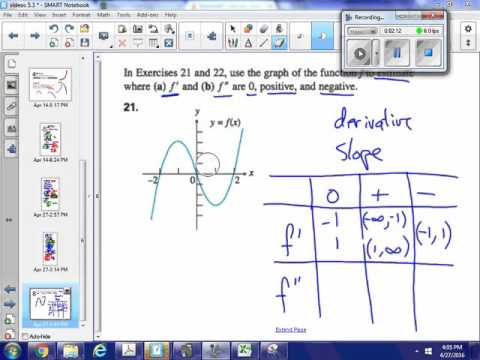 0:04:12
0:04:12
 0:12:49
0:12:49
 0:02:46
0:02:46
 0:08:44
0:08:44
 0:07:29
0:07:29
 0:03:36
0:03:36
 0:02:41
0:02:41
 0:08:55
0:08:55
 0:02:29
0:02:29
 0:08:39
0:08:39
 0:04:44
0:04:44