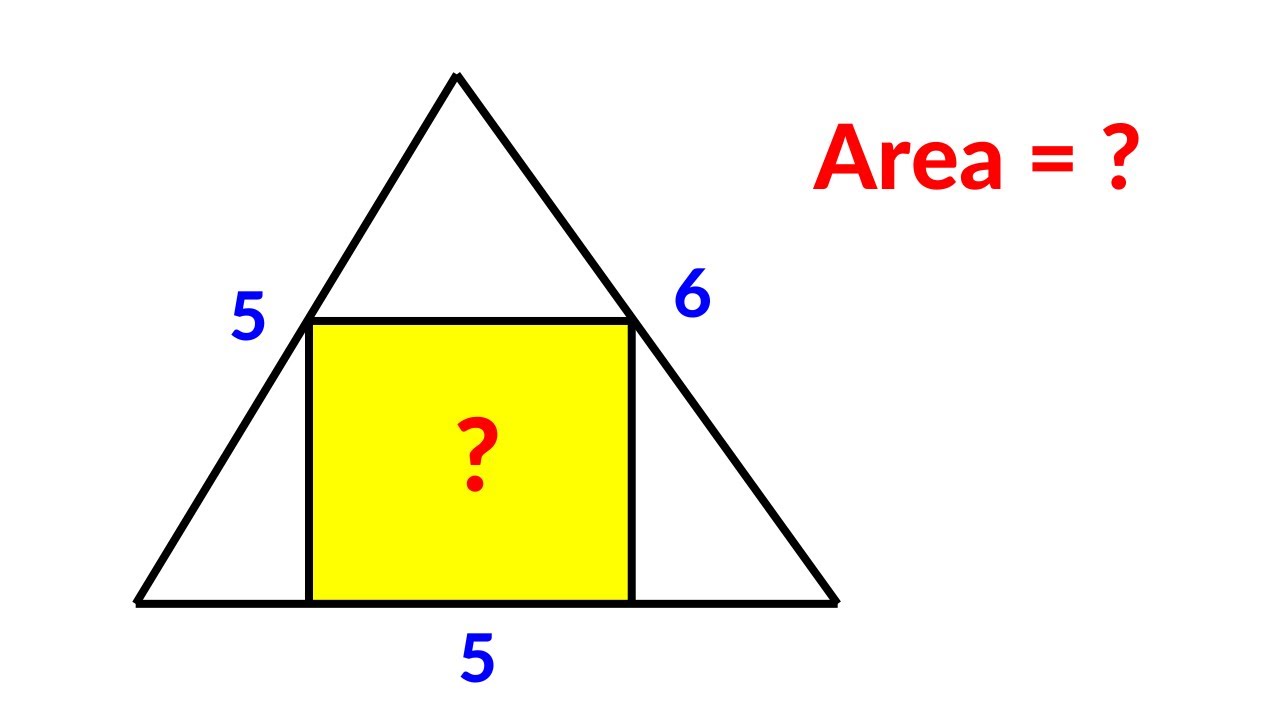
Square inside a triangle | Math Olympiad Geometry Problem

Square inside a triangle | Math Olympiad Geometry Problem

MY OTHER CHANNELS
••••••••••••••••••••••••••••••••

--------------------------------------------------------------------------------

Join the channel to become a member

[juanalfaro]

Let square side = L. Then 5 = L* (cot (B) +1 + cot (C)). Now 6^2 + 5^2 + 5^2 - 2*5*5*cos (B) -> 36 = 25+25 - 2*5*5*cos (B) -> 50-36 = 50*cos (B) = 14 --> cos (B) = 0.28 = 7/25 -> sin (B) = 24/25 -> cot (B) = 7/24. Now 5^2 = 5^2 + 6^2 - 2*5*6*cos (C) -> 25 = 25+36 - 2*5*6*cos (C) -> 36 = 60*cos (C) -> cos (C) = 0.6 -> sin (C) = 0.8 -> cot (C) = 0.6/0.8 = 0.75 = 3/4. Thus L * (7/24 + 1 + 3/4) = 49*L/24 = 5 --> L = 120/49 --> [EDGF] = l^2 = [120/49] ^2 = 14400/2401 = 5.998 (almost 6).

[skwest]

Late, as usual, to this one... and I'm really second-guessing myself, because it shouldn't be this easy...
1. Let's get the area of the triangle from Heron's formula. First off, the semi-perimeter is (5+5+6)/2 = 8. And the formula is √(8•(8-5)•(8-5)•(8-6)), or
√(8•3•3•2) = √(144) = 12.
2. Now drop an altitude from A to segment BC, intersecting (perpendicularly) segment BC at J, and segment ED at H.
3. The length of segment AJ (the altitude) can now be derived from the other formula for the area of a triangle, ½bh. We know the area and the base, so we get this equation:
½(5)h = 12 => 5h = 24 => h = 4.8
4. Next we connect one more segment, FH.
We now have the following 4 right triangles:
△BFE
△EHA
△FJH
△HEF
5. It is a simple matter to establish (via parallels, perpendiculars, corresponding angles, etc.) that these 4 right triangles are all similar to each other by AA.
6. Furthermore, since △BFE and △HEF share a side, EF, they must be congruent. Likewise △EHA and △HEF share side EH, and must, therefore, be congruent. Therefore, by transitivity, △BFE and △EHA are congruent.
7. Finally, that congruency implies that the length of segment FE is equal to the length of segment HA, and that together they sum to the length of the altitude, segment AJ.
If the length of segments FE and HA is x, then we have the equation:
2x = 4.8
or:
x = 2.4
But x is just the length of the side of the square we're interested in. This makes the area we want:
Area = 2.4² = 5.76
And that's our answer.
Now to the video to see if I got it right.
Cheers,
- s.west

[timc]

Thank you for your elegant solution. I think we could also (less elegantly) say:
Let ' S be midpoint of AC, then ASB and CSB are congruent and angle ADB = angle CDB = 90 degrees, so BD = 4, (Pyth.), and
sin(t) = 4/5, cos(t) = 3/5, and
tan(t) = 4/3, (eq'n 1), (t = theta)
sin(B) = sin(180 - 2t) = sin(2t) = 2sin(t)cos(t) = 2(3/5)(4/5), so with '(cos(B)^2 + (sin(B))^ 2 = 1',
sin(B) = 24/25, cos(B) = 7/25, and
tan(t) = 24/7 (eq'n 2)
If square has length 'Y', then from eq'n (1)and (2)
GC = (3/ 4)Y, and BF = (7/24)Y, so
GC + BF + Y = (3/4 + 7/24 + 1)Y = (49/24)Y = 5, so
Area = Y^2 = (120/49)^2
(Alternatively, we might just as easily use cosine rule to get cos(t), cos(B) and thence the other trig. ratios)

2nd Method
Let length of side of square be Y, AP be perpendicular to BC and Q the intersection of AP and ED,
AED and ABC are similar, then
AQ/AP = (ED)/(BC), (eq1)
AP = (AC)sin(t) = (4/5)6 = 24/5, so AQ = 24/5 - Y, so from eq.1:
(24/5 - Y)/(24/5) = Y/5,
1 = (5Y)/24 + Y/5,
(49Y)/120 = 1, so
Area = Y^2 =(120/49)^2

[jonpress]

Draw the altitude from A to BC, intersecting BC at H. By Heron's formula, the area of ABC is 12, so AH = 4.8. By Pythagoras, BH = 1.4 and HC = 3.6. Let s be the side of the square. Triangles BEH, DCH, AED and EDH comprise the totality of ABC, so let's calculate the areas of each of those. The area of BEH is 1.4s/2 = .7s. The area of DCH is 3.6s/2 = 1.8s. The area of AED + EDH is 4.8s/2, The sum of these is 4.9s, which must equal the area of ABC. So s = 12/4.9, which leads to the area of the square: (12/4.9)^2.

[jimlocke]

Drop a perpendicular from B to AC and label the intersection as point M, as done in the video at about 7:35. As explained in the video, CM = 3 and BM = 4. ΔBCM is a 3-4-5 right triangle. Label <BCM as Θ as in the video. The longer side of ΔBCM is opposite Θ. Let the sides of the square have length s. ΔCDG is similar to ΔBCM. DG is opposite Θ, so DG and hypotenuse CD are in the ratio 4:5, making CD 5/4 as long as DG or (5/4)s = (1.25)(s). Drop a perpendicular from A to BC and label the intersection N. Also, label the intersection with DE as P. We note that ΔACN is similar to ΔCDG. Θ is not opposite side CN, so it is the shorter side, so CN = 3/5 AC = (3/5)(6) = 3.6 and CN/BC = 3.6/5. DP and DE are in the same ratio, so DP = (3.6/5) DE = (3.6/5)(s). <ADE = Θ and ΔADE is similar to ΔCDG. DP is not opposite Θ, so is the shorter side, so hypotenuse AD is 5/3 times as long, or (5/3)(3.6/5)(s) = (1.2)(s). CD + AD = AC = 6, so (1.25)(s) + (1.2)(s) = 6, (2.45)(s) = 6, s = 6/(2.45). Multiply numerator and denominator of 6/(2.45) by 20 to get s = 120/49. Area of square = s² = (120/49)², as Math Booster also found.

[Irtsak]

Another solution .
We know the sides of triangle ABC, so we can easily estimate the area of the triangle by Heron’s formula.
(ABC)=12.
So we can find the height AP which corresponds to BC. AP=24/5
Triangles ABP, BEF are similar => AP/EF=AB/BE => EF⋅AB=AP⋅BE =>
x⋅5=24/5 (5-x) => x=120/49

[devondevon]

A different method avoiding using trigonometry

Answer 6 (approximately)
Draw a perpendicular line from BC to A to form two right triangles
Let the height of the left triangle = n, its hypotenuse = 5, and its base is a fraction of 5
Hence the height of the triangle to the right also = n, its hypotenuse = 6 and its base if also a fraction of 5.
Let the base of the triangle to the right = r, then the base of the triangle to the left = 5-r as (5-r + r=5)
Using Pythagorean:
For the triangle to the right, n^2 = 6^2 - r^2
For the triangle to the left n^2 = 5^2 - ([5-r]^2)
Since both = n^2 then

6^2 - r^2 = 5^2 - ([5-r]^2)
36- r^2 = 25 - ( 25-10r + r^2)
36- r^2 = 25 -25 + 10 r - r^2
36 = 10 r
3.6 = r
Hence 5- r = 1.4
hence n =
36- 3.6^2 = n^2
23.06 = n^2
n= 4.8
So the height of the triangle is 4.8 (of course, heron formulae could have been used to get the area,
then divide it by 5 to get 4.8)

Let the side of the square = x since the two triangles that were drawn are similar to the triangles. However, the left triangle is only similar to the triangle to the left, and the right triangle drawn is only
similar to the one to the right.
Hence, for the triangle on the left, its side is 1.4/4.8 of x, and the triangle to the right is 3.6/4.8 of x
1.4/4.8 =0.21967, hence 0.21967 x
3.6/4.8 = 0.75, hence 0.75 x
and side the square = x.
Add these to get 0.21967 x + 0.75x + x = 2.041667 x
Hence 5 (which is the base of the large triangle) = 2.041667x
Hence x = 5/ 2.04166
x =2.44897959, which is the side of the square.
Area= x^2 or 2.44897959^2 = 5.9997 approximately 6 Answer

[DB-lgsq]

شكرا لكم على المجهودات
يمكن استعمال x=ED
S(ABC)=12
sinBAC=24/25 =x/5-x
x=120/49

[lashman]

The area surface of triangle is 12, then height from A is 4, 8. If x is a side of the square, then 4, 8/5=(4, 8-x)/x from similar triangles. x=2, 449 and S=5, 998

[ciricola]

ΔABC is an isosceles triangle. The lengths of the three sides are known; and its three
angles can be easily calculated: 53.1°, 53.1°, 73.8°; ∠ABF = 73.8°

ΔAED is a triangle similar to ΔABC; designate side AE of ΔAED as (length) V. Then, line segments ED, DG, FG, EF are all equal to V (in length)

For ΔBEF, let line segment BE = T; ∠EBF = 73.8°, sin 73.8° = .96 = V/T

T = V/.96 = 1.04V

V + T = 5, V + 1.04V = 5, 2.04V = 5, so V=2.45

Area of square = V² =(2.45)² = 6

[Irtsak]

2nd solution .
Triangle ABC is isosceles . Let BK is the heigh which corresponds to AC. So AK=3
By Pethagoras theorem in Δ ABK => BK=4 and very easily *(ABC)=12*

*Τhe ratio of the areas of two similar triangles is equal to the square of the similarity ratio*
Triangles AED, ABC are similar => (AED)/(ABC)=λ²
However λ = x/5 => ((AED))/((ABC) )=(x/5)² => *(AED)=12•x²/25*
Notice that (BEDC)+(AED) =(ABC) => ((BC+ED)⋅EF)/2+12⋅x^2/25=12 =>
((5+x)⋅x)/2+(12x^2)/25=12 ……………….. *x=120/49*

[istvanherenyi]

Let x the length of ED. The area of ABC is T=12 (Heron). Area of AED is t1. t1/T=x^2/25, t1=12*x^2/25. Let t2 the sum of area BEF and GDC. t2/T=(5-x)^2/25, t2=12*(5-x)^2/25. t1 + t2 +x^2=T=12, so 49x^2 - 120x=0 and x=0 or 120/49.

[AndreasPfizenmaier-yw]

BM=4 Hence cos 36, 9 =BG:4 Hence DG=2, 4

[RobG]

It would've been as easy to show ∆AED was similar to ∆ABC because ED is parallel to BC so angle ADE will be equal to angle ACB.