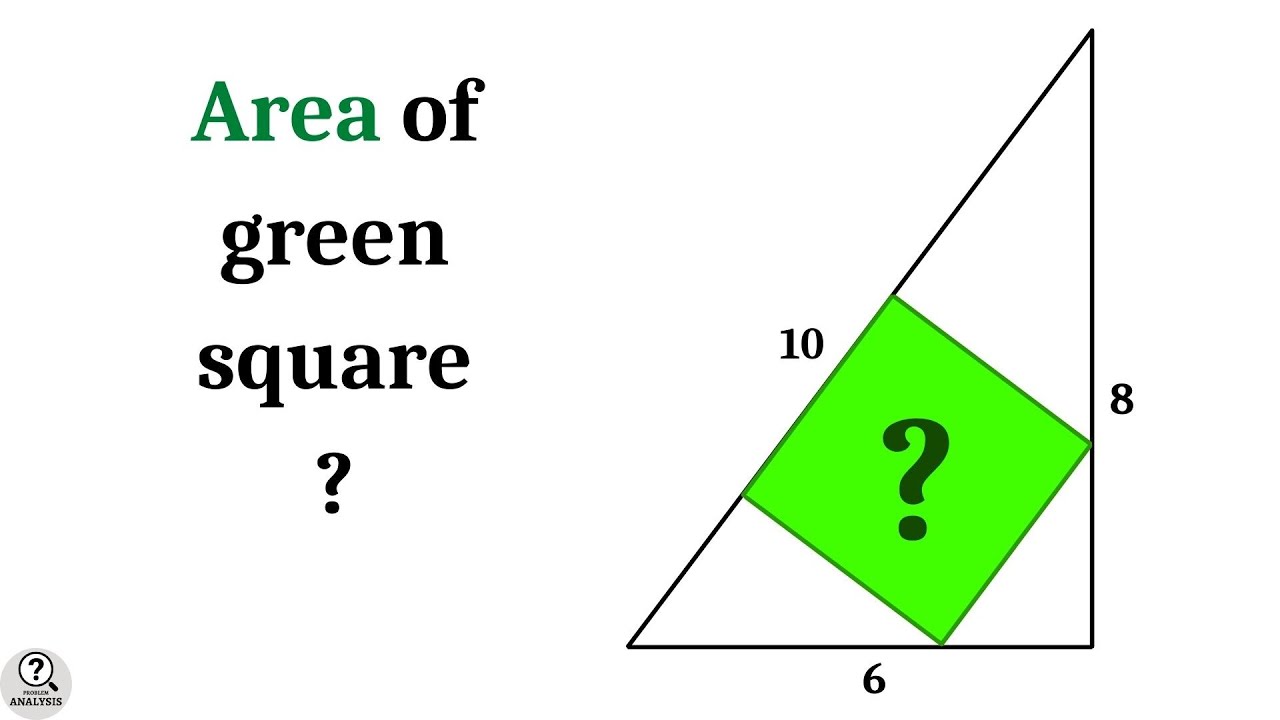
Square inside right triangle problem | Geometry | Advanced math problems | Mathematics

There are a bunch of problems which are seem to be very advanced, but only basic knowledge are required to solve. This problem is an application of the concept of similar triangles. Basic ideas about right triangles and similarity of triangles are needed to solve this problem.

Any queries regarding the subject or videos are invited.
Instagram ID : problem_analysis

#maths #mathematics #triangle #square #area #algebra #calculation #problems #geometry

[TATARLaine]

You can go the trig way is observing cos(x)=8/10 and sin(x)=6/10 you can split the AB side in two of length t and u and then sin(x)=a/t and cos(x)=u/a
multiply both sides sin(x)*cos(x)=u/t => u =(48/100)t
we know the t+u=8=t+(48/100)t=(148/100)*t
t = 800/148 and a=sin(x)*t=(6/10)*(800/148) = (6*80)/148=120/37

[KrishnaShashank-bo]

i used straight lines by taking that entire thing into coordinate system and i still got the right answer!!!!

[shadrana]

At 3:26,
Consider square PQRS,
Let side = a,
IPQRSI=
IABCI = AB*BC/2 = 8*6/2
All the triangles are similar (equal angles)
Consider triangle RBS,
AC/SR = AB/RB, (triangles are similar)
10/a= 8/RB RB= 4a/5
AC/SR = CB/SB, (triangles are similar)
10/a= 3a/5
IRBSI = (RB*SB)/2 = (4a/5)(3a/5)/2 =
Consider triangles AQR and CPS,
IAQRI+ICPSI =
IABCI = IRBSI+IAQRI+ICPSI+IPQRSI
24= 6a^2/25+a(10-a)/2+
(5) comes down to the quadratic,
37a^2+250a-1200 =0
(37a-120)(a+10)=0
a= 120/37 since the a= -10 has to be rejected.
IPQRSI= a^2 =(120)^2/37^2 = 10.51862673 square units approx.