filmov
tv
Graphical convolution example

Показать описание
Learn how to apply the graphical "flip and slide" interpretation of the convolution integral to convolve an input signal with a system's impulse response.
Convolution integral example - graphical method
Graphical convolution example
Graphical Convolution Integral
Convolution in 5 Easy Steps
Discrete Time Convolution Example
But what is a convolution?
Signals & Systems - Graphical Procedure to Perform Convolution - working examples - 1 - UNIT III
Graphical Convolution with Examples
Introduction to Convolution Operation
Graphical Convolution : Example 03
Continuous-Time Convolution 1
L.T. - Graphical Convolution Example
Graphical Convolution : Example 07
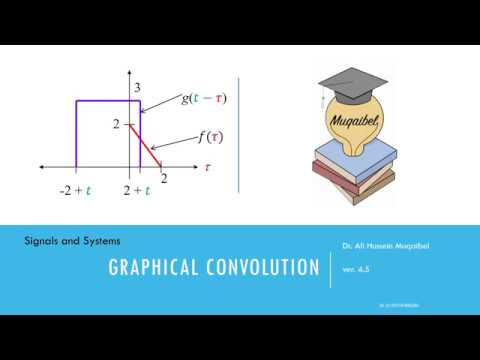
Graphical Convolution
Convolution by Image Method
Graphical Method of Convolution || The Convolution Integral || Practice Problem 15.12 || ENA 15.5(2)
Convolution by graphical method
Graphical Convolution : Example 02
Graphical Convolution: Example 01
Graphical #Convolution #Animation
#110 Solved problems -2 on Convolution Sum || EC Academy
Graphical convolution example
#112 Solved Problems on Convolution Integral // EC Academy
Convolution Integral || Graphical Method of Convolution || Example 15.12 || ENA 15.5(1a)(English)
Комментарии
 0:15:56
0:15:56
 0:11:16
0:11:16
 0:11:40
0:11:40
 0:14:02
0:14:02
 0:10:10
0:10:10
 0:23:01
0:23:01
 0:10:06
0:10:06
 0:23:52
0:23:52
 0:30:42
0:30:42
 0:13:05
0:13:05
 0:28:50
0:28:50
 0:16:17
0:16:17
 0:15:04
0:15:04
 0:18:44
0:18:44
 0:13:42
0:13:42
 0:11:09
0:11:09
 0:10:03
0:10:03
 0:16:16
0:16:16
 0:09:30
0:09:30
 0:01:30
0:01:30
 0:12:24
0:12:24
 0:03:27
0:03:27
 0:15:10
0:15:10
 0:10:47
0:10:47