Missing Point of a Parallelogram | Problem of the day

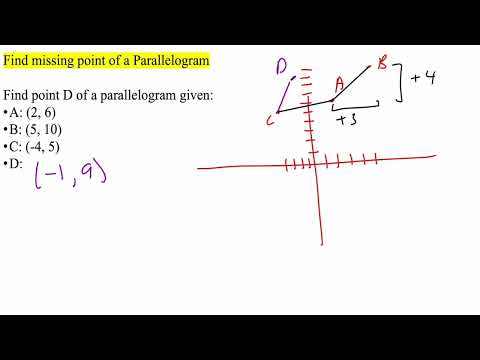
In parallelogram ABCD as opposite sides are parallel, compare triangles ABC and CDA. In these triangles AC = CA (common sides). Also ∠BAC =∠DCA (alternate interior angles), and ∠BCA = ∠DAC (alternate interior angles). Hence by the ASA criterion, both the triangles are congruent and the corresponding sides are equal. Therefore we have AB = CD, and BC = AD.

Few questions look simple, but when it comes to code, we miss some of the cases, and this video is a perfect example of one such problem that was asked in an interview at Morgan Stanley.

Let us know if you have any questions related to explanation or understanding in the comments section.

Solve this problem on our practice portal:

Follow us on our Social Media Handles -

Also, Subscribe if you haven't already! :)

[raviagrawal]

Why can't we use midpoint theorem to calculate D.
x4 = x1 + x3 - x2;
x5 = x2 + x3 - x1;
x6 = x1 + x2 - x3;
and similarly for their y-coordinates.
and the we will compare P4, P5 and P6 lexicographically.