filmov
tv
Rational Roots Proof

Показать описание
Rational Roots Theorem Proof
In this video, I prove the rational roots theorem, which is a neat way of finding rational roots of polynomials. A little algebra delight to sweeten the day!
In this video, I prove the rational roots theorem, which is a neat way of finding rational roots of polynomials. A little algebra delight to sweeten the day!
Rational Roots Proof
Proof of Rational Root Theorem
Rational Root Theorem
Proof of the Rational Root Theorem
Can You Prove that a polynomial has no rational roots?
How to prove that an equation has rational roots
Sqrt of 2 is irrational[ Proof by Rational Root Theorem]
RATIONAL ROOT THEOREM 🔥🔥 Proof Explained with Example | Finding rational zeros of Polynomials
Precalc C - Rose - Proof of the Rational Root Theorem
The Rational Root Theorem -- How and Why
Prove Sin(10 degrees) Is Irrational | Using Rational Root Theorem.
Rational Root theorem prove and examples
Rational Root Theorem, with Proof
Rational Roots Test / Theorem
Polynomials: Using the Rational Root Theorem to Prove Irrationality
Prove that the Set of all Positive Rationals with Rational Roots is a Group
Proof of the Rational Roots Theorem
A Proof That The Square Root of Two Is Irrational
Rational Roots Theorem
Rational Zeros Theorem Proof
Don’t even attempt Quartic Formula - Rational Root Theorem is best! #mathematics #algebra2
Rational Root Theorem - Finding the list of all possible rational roots
Rational Root Test - Precalculus
Rational Roots Putnam Problem
Комментарии
 0:11:47
0:11:47
 0:19:28
0:19:28
 0:06:02
0:06:02
 0:07:28
0:07:28
 0:06:41
0:06:41
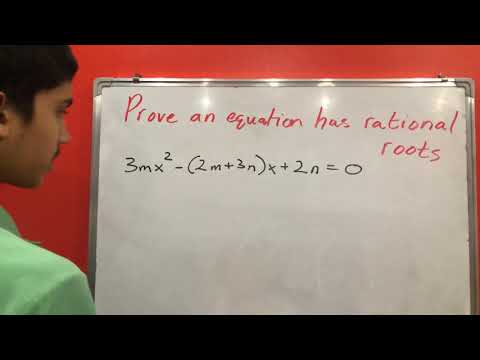 0:01:26
0:01:26
 0:05:40
0:05:40
 0:16:19
0:16:19
 0:29:52
0:29:52
 0:13:39
0:13:39
 0:03:21
0:03:21
 0:07:24
0:07:24
 0:13:58
0:13:58
 0:06:51
0:06:51
 0:03:20
0:03:20
 0:09:56
0:09:56
 0:02:59
0:02:59
 0:17:22
0:17:22
 0:12:40
0:12:40
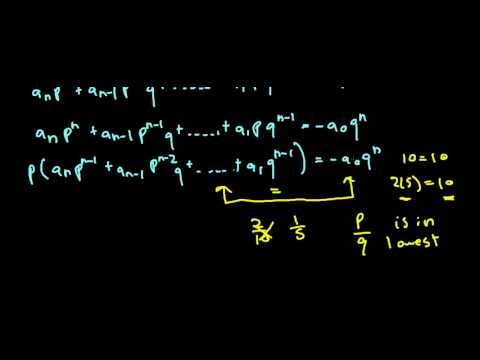 0:14:52
0:14:52
 0:01:00
0:01:00
 0:02:52
0:02:52
 0:00:33
0:00:33
 0:15:02
0:15:02