filmov
tv
PDF Sampling: MCMC - Metropolis-Hastings algorithm
Показать описание
Probability density function sampling using Markov-Chain Monte Carlo: Metropolis-Hastings algorithm
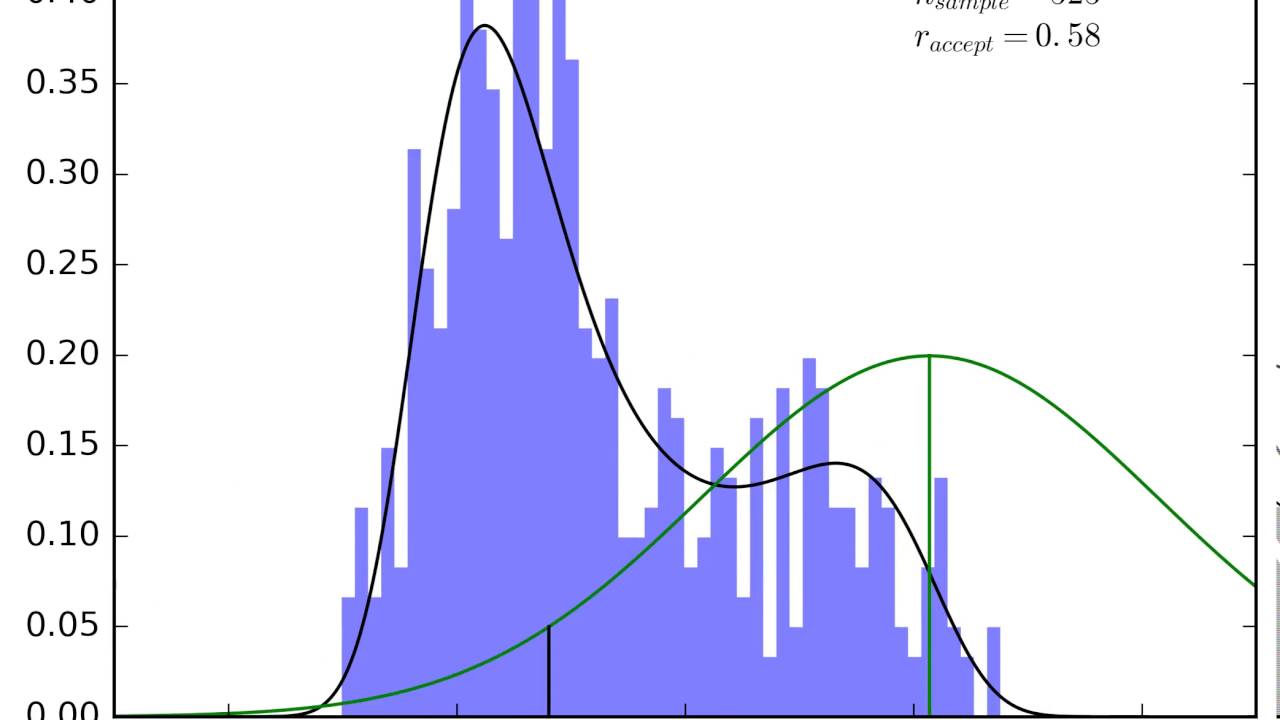
Green curve is the proposed distribution.
Green vertical line is the position of last state
Black vertical line is the proposed state that accepted
Red vertical line is the position of the last state that become a sample again because proposed state is rejected
Green curve is the proposed distribution.
Green vertical line is the position of last state
Black vertical line is the proposed state that accepted
Red vertical line is the position of the last state that become a sample again because proposed state is rejected
0:00:41
PDF Sampling: MCMC - Metropolis-Hastings algorithm
0:08:14
Introduction to Bayesian statistics, part 2: MCMC and the Metropolis–Hastings algorithm
0:09:49
Understanding Metropolis-Hastings algorithm
1:18:01
Lecture 16. Gibbs Sampling
1:59:42
Machine Learning II Lecture 9
0:24:45
Metropolis-Hastings - VISUALLY EXPLAINED!
0:11:28
An introduction to the Random Walk Metropolis algorithm
0:08:19
MCMC (7): The Metropolis-Hastings method
0:01:50
Metropolis-Hastings sampling algorithm
0:12:12
Advanced Bayesian Methods: Metropolis Hastings
0:12:04
39 - Metropolis Hastings
0:24:04
Metroplis-Hastings independence sampler example
0:08:49
Gibbs Sampling : Data Science Concepts
0:19:30
Metropolis Hasting algorithms under MCMC
0:44:03
A Beginner's Guide to Monte Carlo Markov Chain MCMC Analysis 2016
0:00:50
Metropolis Hastings sampling
0:44:45
Optimization of Proposal Distribution for the Metropolis-Hastings Algorithm
1:59:55
M4 | MCMC sampling & Optimization methods | CIV6540E
1:18:18
Lecture 17. Markov Chain Monte Carlo and Metropolis-Hasting Algorithm
0:05:26
Using the Random Walk Metropolis algorithm to sample from a cow surface distribution
0:01:30
Metropolis-Hastings MCMC Demo
1:43:59
2023-01-23 PRML - MCMC
0:46:57
Metropolis Hastings MCMC
0:06:32
Markov Chain Monte Carlo: Metropolis-Hastings-Sampler Part1
Комментарии