filmov
tv
[Discrete Mathematics] Permutations and Combinations Examples 2

Показать описание
In this video we do a letter permutation problem, a random walk problem, and a circular table problem.
LIKE AND SHARE THE VIDEO IF IT HELPED!
*--Playlists--*
*--Recommended Textbooks--*
Hello, welcome to TheTrevTutor. I'm here to help you learn your college courses in an easy, efficient manner. If you like what you see, feel free to subscribe and follow me for updates. If you have any questions, leave them below. I try to answer as many questions as possible. If something isn't quite clear or needs more explanation, I can easily make additional videos to satisfy your need for knowledge and understanding.
LIKE AND SHARE THE VIDEO IF IT HELPED!
*--Playlists--*
*--Recommended Textbooks--*
Hello, welcome to TheTrevTutor. I'm here to help you learn your college courses in an easy, efficient manner. If you like what you see, feel free to subscribe and follow me for updates. If you have any questions, leave them below. I try to answer as many questions as possible. If something isn't quite clear or needs more explanation, I can easily make additional videos to satisfy your need for knowledge and understanding.
[Discrete Mathematics] Permutations and Combinations Examples
Discrete Math - 6.3.1 Permutations and Combinations
Permutations and Combinations Tutorial
Discrete Math 6.3.1 Permutations and Combinations
Complete Permutation & Combination concept in 1️⃣ Shot
Introduction to Permutations and Combinations
Difference Between Permutations and Combinations | Discrete Math Exercises
Permutations, Combinations & Probability (14 Word Problems)
[Discrete Mathematics] Permutation Practice
The Counting Principle, Permutations, and Combinations
Permutations & Combinations | Chapter-9 | Discrete Mathematics | nesoacademy.org
COMBINATIONS with REPETITION - DISCRETE MATHEMATICS
Permutations and Combinations | Counting | Infinity Learn
Discrete Mathematics | MA3354|Combinatorics| Permutations & Combinations |Introduction with exam...
Statistics, Permutations vs Combinations | Apna Teacher
COMBINATORICS | PERMUTATIONS | COMBINATIONS | PERMUTATIONS AND COMBINATIONS | DISCRETE MATHEMATICS |
Question on Probability, Permutation and Combination | Discrete Mathematics | UGC NTA NET May 2021
COMBINATIONS - DISCRETE MATHEMATICS
How to tell the difference between permutation and combination
Permutation and Combination one shot with PYQs and MCQs | Discrete Math
How to Use Permutations and Combinations
Introduction To Permutations And Combinations Explained in Hindi l Aptitude Course
PERMUTATIONS and COMBINATIONS Review - Discrete Mathematics
Permutations, Combinations, and Probability (15 Word Problems)
Комментарии
![[Discrete Mathematics] Permutations](https://i.ytimg.com/vi/FCYj10HuA_E/hqdefault.jpg) 0:04:45
0:04:45
 0:14:48
0:14:48
 0:17:41
0:17:41
 0:13:35
0:13:35
 0:33:46
0:33:46
 0:10:05
0:10:05
 0:15:11
0:15:11
 0:21:17
0:21:17
![[Discrete Mathematics] Permutation](https://i.ytimg.com/vi/aqTzHOvabYM/hqdefault.jpg) 0:14:41
0:14:41
 0:07:39
0:07:39
 0:01:24
0:01:24
 0:13:35
0:13:35
 0:05:40
0:05:40
 0:08:27
0:08:27
 0:07:08
0:07:08
 0:13:19
0:13:19
 0:06:24
0:06:24
 0:17:38
0:17:38
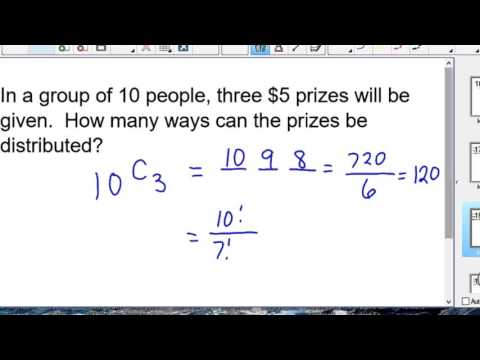 0:08:51
0:08:51
 1:24:11
1:24:11
 0:07:37
0:07:37
 0:09:30
0:09:30
 0:24:15
0:24:15
 0:43:24
0:43:24