filmov
tv
The set of rational numbers is a field: Wrong answers
Показать описание
To show that a set is a field, we need to check all the axioms of the field CONCRETELY. Just listing the axioms is not a proof.
0:02:39
11 Set of Rational Numbers
0:08:51
Integers & Rationals are both infinite but is it the SAME infinity?
0:09:54
Rational Numbers Explained | Math with Mr. J
0:05:54
Rational and Irrational Numbers
0:18:08
Rational Numbers
0:02:29
What are Rational Numbers? | Number System Concept | Infinity Learn
0:03:30
Prove that the Set of All Rational Numbers Between 0 and 1 Inclusive is Countable
0:09:36
Which set is bigger: the integers or the rational numbers?
0:09:47
For every real number 𝑥, there is a set of rational numbers whose least upper bound is exactly x.
0:09:00
What are the Types of Numbers? Real vs. Imaginary, Rational vs. Irrational
0:00:16
Number System ( Natural Number, Whole Number, Integer, Rational Number, Irrational Number, Real)
0:04:36
Learn the Types of Numbers - Natural, Whole, Integers, Rational, Irrational, Real, Imaginary
0:07:58
Classification of Numbers (Natural, Whole, Integers, Rational, Irrational, Real) - Nerdstudy
0:17:10
The set of rational numbers is a field: Wrong answers
0:17:31
An Intro to Rational and Irrational Numbers | Math with Mr. J
0:00:16
Rational Numbers
0:03:42
Set of Real Numbers | Subsets of Real Numbers | Set Symbols in Math [Animated] - Pre-Algebra
0:00:10
Rational number identify #quiz #mathematics
0:01:08
What does Z, N, Q and R stand for in set notation
0:23:41
Section 6.1: The Set of Rational Numbers (UNEDITED)
0:00:05
properties of rational numbers in whole numbers
0:04:44
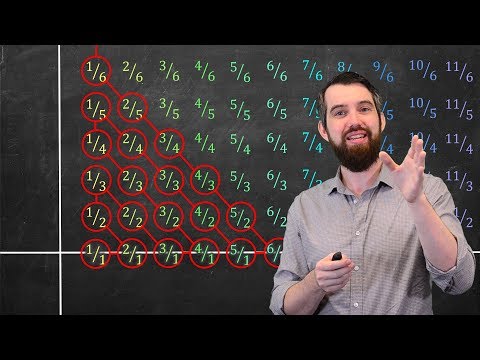
Rational Numbers are Countable
0:00:10
|| Number System || #numbers #maths #mathematics #digit #ssc
0:06:13
Algebra I #2.5e, Set Notation and Subsets of rational numbers
Комментарии