filmov
tv
Which set is bigger: the integers or the rational numbers?

Показать описание
Which set is bigger: the integers or the rational numbers?
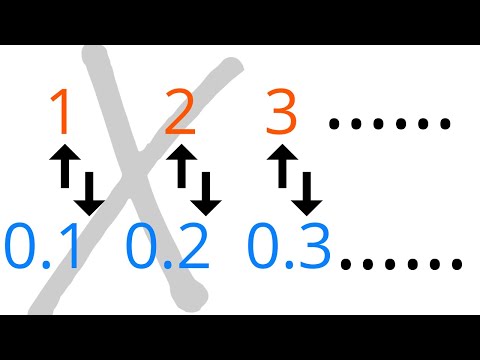
Which Set is Bigger? N vs Q
A set larger than R
How Irrational Infinite Set Is Bigger Than Natural Infinite Set...
10 Upcoming Games BIGGER Than Planet Earth
Circle bigger number in each set.#Funtvwithshreyansh☀️🍆☕
The last line was set too a 7 in bigger HORSE strides but… I got a 5 🫣
Giant-Set For Bigger Forearms⚠️😮💨
Ichiban Kuji Dragon Ball VS Omnibus COMPLETE SET REVIEW!!!
Giant-Set for BIGGER Triceps #triceps #workout #gymmotivation
Unlock a BIGGER Turn In The Backswing With This Set Up!
Build Bigger Shoulders With This Cable Set Up
Building a LEGO Set EVERY Day but Each Day it Gets BIGGER! | Day 31
LEGO, but Each Day the Set gets BIGGER...
Building a LEGO Set EVERY Day but Each Day it Gets BIGGER! | Day 24
BUILD A BIGGER CHEST BENCH PRESS ROUTINE (EVERY REP & SET) | WITH MIKE RASHID
'Avengers: Age of Ultron' On-Set Exclusive: What Makes the Sequel Bigger & Better?
Why You Need To Set A Bigger Goal
Set A Bigger Table: Seafood
Do you want a Lego set bigger #legosets #starwar #legotoys #legomania #funnylego
Just made this set bigger 🙌 Do you like it?
When you become iconic, you become bigger than the role you set out to play #brandstorytelling
Cherry blossom set. Very soon I will upload bigger sets #lego
THE WORLD’S LARGEST MALL SET TO GET EVEN BIGGER
Комментарии
 0:09:36
0:09:36
 0:00:58
0:00:58
 0:20:36
0:20:36
 0:00:56
0:00:56
 0:16:24
0:16:24
 0:00:16
0:00:16
 0:00:32
0:00:32
 0:00:29
0:00:29
 0:18:04
0:18:04
 0:00:08
0:00:08
 0:08:01
0:08:01
 0:00:32
0:00:32
 0:00:55
0:00:55
 0:18:31
0:18:31
 0:00:33
0:00:33
 0:11:40
0:11:40
 0:03:19
0:03:19
 0:00:48
0:00:48
 0:00:21
0:00:21
 0:00:15
0:00:15
 0:00:05
0:00:05
 0:00:17
0:00:17
 0:00:16
0:00:16
 0:00:55
0:00:55