Understanding Trig Values & the Unit Circle

The unit circle is like the Swiss Army knife of trigonometry—compact, versatile, and incredibly useful. Imagine a circle with a radius of exactly one unit, centered at the origin of a coordinate plane. This simple shape unlocks a treasure trove of mathematical relationships.

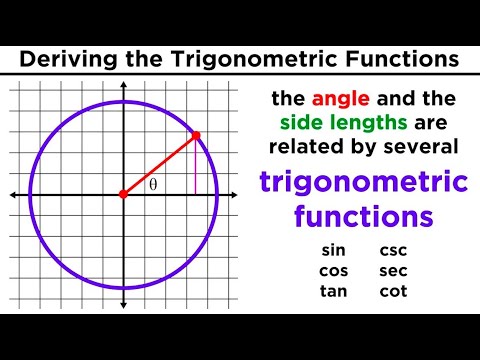
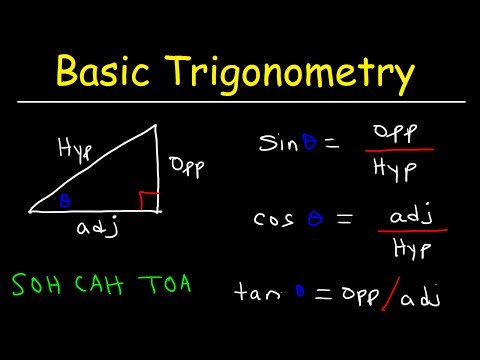
The beauty of the unit circle lies in how it connects angles to coordinates. Any point on the circle corresponds to an angle, measured from the positive x-axis, and has coordinates (cos θ, sin θ), where θ is the angle in radians. This means the x-coordinate of any point on the unit circle is the cosine of the angle, and the y-coordinate is the sine.

But the unit circle isn’t just about coordinates—it’s a powerful tool for understanding trigonometric functions and their behavior. For example, as you move around the circle, you can see how the sine and cosine values fluctuate between -1 and 1, illustrating the periodic nature of these functions.

The unit circle also helps you visualize important trigonometric identities, like how sine and cosine are complementary. It’s your go-to guide for solving equations, understanding angles, and navigating the complexities of trigonometry with confidence and clarity.

[goldenfox]

What’s crazy is I was trying to do this and by myself I came up with sqrt(2)/2 during class today

[jeffreypullis]

Cool. I never knew what sine and cosine were!

[dablakhl]

Don't tell this to flat earthers, it will cause their tiny brains to explode.

[jesseeganpoirier]

Am I the only one who remembers this as route 4, 3, 2, 1 over 2?

[idjles]

Wow, this was a sloppy and rambly mess.