filmov
tv
Jordan-Normalform - Teil 1 - Überblick

Показать описание
Abonniert den Kanal oder unterstützt ihn auf Steady:
Ihr werdet direkt informiert, wenn ich einen Livestream anbiete.
Hier erzähle ich etwas über die Jordan-Zerlegung von quadratischen Matrizen bzw. die jordansche Normalform im Allgemeinen.
(Aufgabe passt zur Vorlesungen wie Mathematik für Ingenieure, Mathematik für Physiker, Mathematik für Naturwissenschaftler, Mathematik für Wirtschaftswissenschaftler und natürlich auch für Mathematik-Vorlesungen für Mathematiker)
Jordan-Normalform - Teil 1 - Überblick
Jordan-Normalform - Teil 1 - Überblick
Jordan Normalform, einfaches Aufstellen, Lineare Algebra | Mathe by Daniel Jung
Jordan Normalform Beweis Teil 1: Lemma von Fitting Lineare Algebra
Jordan-Normalformen
Jordan Normalform, Übersicht mit Diagonalmatrix, Lineare Algebra | Mathe by Daniel Jung
Jordan Normalform, Vielfachheit, algebraisch, geometrisch, Lineare Algebra | Mathe by Daniel Jung
Jordan Normalform, Eigenwerte, Kästchen, Blöcke, Lineare Algebra | Mathe by Daniel Jung
Jordan-Normalform - Teil 4 - Transformationsmatrix aufstellen
Teil 21: Beweis der Jordan'schen Normalform
Jordan Normalform: Lemma von Fitting - Antwort auf eine Zuschauerfrage
Jordan-Normalform - Teil 2 - Beispiel
Jordan-Normalform - Teil 3 - Ein weiteres Beispiel
Jordansche Normalform
Jordan Normalform bestimmen (Beispiel 3x3)
Teil 20: Die Jordan'sche Normalform
Aufgabe 7.4.7, Jordan-Normalform, Lineare-Algebra-Buch (Kemper, Reimers)
Jordan Normalform Beweis Teil 2: Hauptraumzerlegung Lineare Algebra
Jordan-Normalform - Teil 4 - Transformationsmatrix
Die Jordan Normalform vs Diagonal-Gestalt einer Matrix/Die Jordan Basis
Jordansche Normalform einer 3x3 Matrix mit Parameter | Übung mit Lösung (Lineare Algebra)
Jordan-Normalform - Teil 3 - Ein weiteres Beispiel
Spur einer Matrix und Jordansche Normalform ist gleich - Beweis (Lineare Algebra)
LAII 006 Jordan normal form
Комментарии
 0:21:16
0:21:16
 0:21:16
0:21:16
 0:03:36
0:03:36
 0:10:09
0:10:09
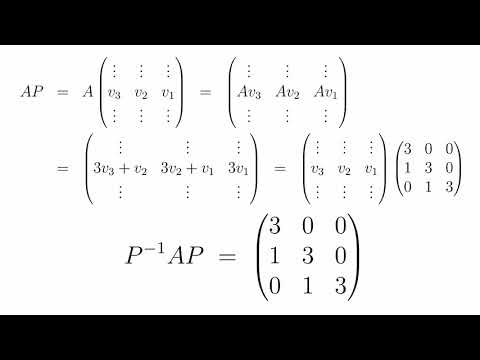 0:29:35
0:29:35
 0:05:29
0:05:29
 0:04:31
0:04:31
 0:03:02
0:03:02
 0:29:31
0:29:31
 1:01:16
1:01:16
 0:03:41
0:03:41
 0:17:13
0:17:13
 0:12:16
0:12:16
 0:14:45
0:14:45
 0:12:01
0:12:01
 0:25:49
0:25:49
 0:36:51
0:36:51
 0:11:55
0:11:55
 0:29:31
0:29:31
 0:06:46
0:06:46
 0:06:45
0:06:45
 0:12:16
0:12:16
 0:02:50
0:02:50
 0:06:05
0:06:05