QIP 2021 | Bipartite energy-time uncertainty relation for quantum metrology with... (Philippe Faist)

Bipartite energy-time uncertainty relation for quantum metrology with noise

Authors: Philippe Faist, Mischa Woods, Victor V. Albert, Joseph M. Renes, Jens Eisert and John Preskill
Affiliations: Freie Universität Berlin | ETH Zurich | National Institute of Standards and Technology, Gaithersburg, MD | ETH Zurich | FU Berlin | Caltech

Abstract:
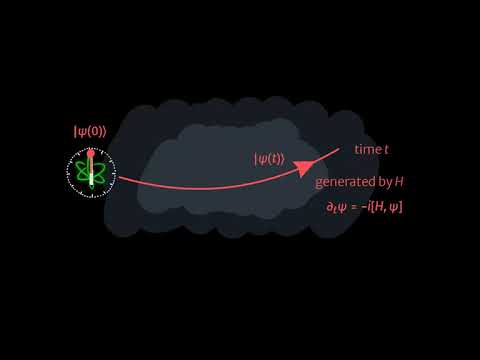
Noise in quantum metrology reduces the sensitivity to which one can determine an unknown parameter in the evolution of a quantum state, such as time. Here, we consider a probe system prepared in a pure state that evolves according to a given Hamiltonian. We study the resulting local sensitivity of the probe to time after the application of a given noise channel. We show that the decrease in sensitivity due to the noise is equal to the sensitivity that the environment gains with respect to the energy of the probe. We obtain necessary and sufficient conditions for when the probe does not suffer any sensitivity loss; these conditions are analogous to, but weaker than, the Knill-Laflamme quantum error correction conditions. New upper bounds on the sensitivity of the noisy probe are obtained via our uncertainty relation, by applying known sensitivity lower bounds on the environments system. Our time-energy uncertainty relation also generalizes to any two arbitrary parameters whose evolutions are generated by Hermitian operators. This uncertainty relation asserts a general trade-off between the sensitivities that two parties can achieve for any two respective parameters of a single quantum system, in terms of the commutator of the associated generators. We consider applications to strongly interacting many-body probes. We find probe states for general interaction graphs of Ising and Heisenberg interactions that are robust to any single located error. For a 1D spin chain with nearest-neighbor interactions subject to amplitude damping noise on each site, we verify numerically that our probe state does not lose any sensitivity to first order in the noise parameter.

Get entangled with us!