filmov
tv
im(T): Image of a transformation | Matrix transformations | Linear Algebra | Khan Academy

Показать описание
Showing that the image of a subspace under a transformation is also a subspace. Definition of the image of a Transformation.
Missed the previous lesson?
Linear Algebra on Khan Academy: Have you ever wondered what the difference is between speed and velocity? Ever try to visualize in four dimensions or six or seven? Linear algebra describes things in two dimensions, but many of the concepts can be extended into three, four or more. Linear algebra implies two dimensional reasoning, however, the concepts covered in linear algebra provide the basis for multi-dimensional representations of mathematical reasoning. Matrices, vectors, vector spaces, transformations, eigenvectors/values all help us to visualize and understand multi dimensional concepts. This is an advanced course normally taken by science or engineering majors after taking at least two semesters of calculus (although calculus really isn't a prereq) so don't confuse this with regular high school algebra.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Missed the previous lesson?
Linear Algebra on Khan Academy: Have you ever wondered what the difference is between speed and velocity? Ever try to visualize in four dimensions or six or seven? Linear algebra describes things in two dimensions, but many of the concepts can be extended into three, four or more. Linear algebra implies two dimensional reasoning, however, the concepts covered in linear algebra provide the basis for multi-dimensional representations of mathematical reasoning. Matrices, vectors, vector spaces, transformations, eigenvectors/values all help us to visualize and understand multi dimensional concepts. This is an advanced course normally taken by science or engineering majors after taking at least two semesters of calculus (although calculus really isn't a prereq) so don't confuse this with regular high school algebra.
About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.
For free. For everyone. Forever. #YouCanLearnAnything
Комментарии
 0:16:37
0:16:37
 0:06:06
0:06:06
 0:10:34
0:10:34
 0:05:19
0:05:19
 0:06:09
0:06:09
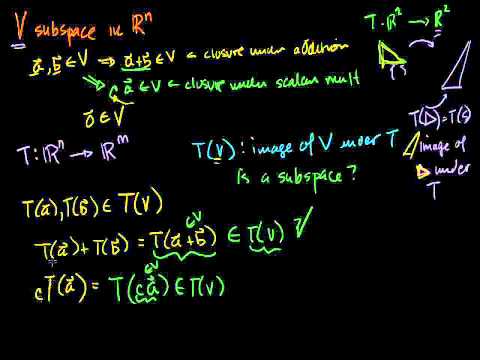 0:16:43
0:16:43
 0:08:25
0:08:25
 0:06:14
0:06:14
 0:18:11
0:18:11
 0:04:27
0:04:27
 0:04:33
0:04:33
 0:18:47
0:18:47
 0:08:46
0:08:46
 0:15:49
0:15:49
 0:05:19
0:05:19
 0:04:06
0:04:06
 0:03:04
0:03:04
 0:06:36
0:06:36
 0:04:16
0:04:16
 0:12:10
0:12:10
 0:02:53
0:02:53
 0:10:12
0:10:12
 0:11:28
0:11:28
 0:12:09
0:12:09