filmov
tv
ЯПОНСКАЯ ЗАДАЧА XVI века!

Показать описание
ЯПОНСКАЯ ЗАДАЧА XVI века!
Известная японская задача по геометрии ➜ Найдите площадь прямоугольника на рисунке...
Япония XVII-XVIII века.
Короткие загадки, которые осилит не каждый профессор
ПОЧЕМУ САМОЛЕТЫ НЕ ЛЕТАЮТ НАД ТИХИМ ОКЕАНОМ? 6 секретов авиаперелетов...
36 Скрытых Секретов на Вещах, которым вы пользуетесь каждый день...
Японская керамика XIII века – вызов современности
История России. ХХ век. Лекция 16. Коллективизация | History Lab...
25 Мастеров Иллюзии, Которые Взорвут Ваш Мозг
История Кореи на карте.
Самые Слабые Армии в Мире
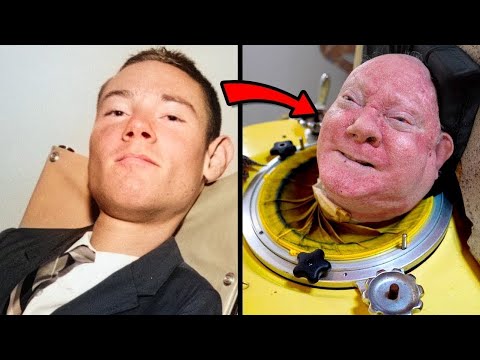
Он Находится в Этом Аппарате Уже 70 Лет
Первая русская экспедиция в Японию. Южный отряд Шпанберга. Часть (3/5)...
ПАНИКА в России: США Испытывают Новый Истребитель 6-го Поколения Стоимостью 150 Миллионов Долларов...
Население России наглядно за 6 минут
Japan: History, Geography, Economy & Culture
Востоковедение и история в современной науке о мире (лекция А.И. Фурсова в Школе востоковедения ВШЭ)...
АРМИЯ ПРОШЛО И АРМИЯ БУДУЩЕГО ( UEBS 2 )
Почему люди обожают Японию | ФАЙБ
Что же случилось в начале 19 века?
Самурай без меча. Китами Масао. [Аудиокнига]
Как спаситель АвтоВАЗа стал преступником в Японии. Невероятная история Карлоса Гона...
Перл Харбор: ужасное поражение или провокация?
История Норвегии за 16 минут
Комментарии
 0:10:45
0:10:45
 0:02:37
0:02:37
 0:08:51
0:08:51
 0:10:12
0:10:12
 0:10:24
0:10:24
 0:19:07
0:19:07
 0:53:04
0:53:04
 0:13:05
0:13:05
 0:09:33
0:09:33
 0:16:41
0:16:41
 0:16:30
0:16:30
 0:19:16
0:19:16
 0:33:36
0:33:36
 0:12:34
0:12:34
 0:06:23
0:06:23
 0:32:26
0:32:26
 0:50:48
0:50:48
 0:20:33
0:20:33
 0:32:41
0:32:41
 0:23:55
0:23:55
 1:44:13
1:44:13
 0:32:51
0:32:51
 0:41:49
0:41:49
 0:16:57
0:16:57