filmov
tv
Simplify the rational expression by factoring the polynomial – MUST KNOW ALGEBRA!
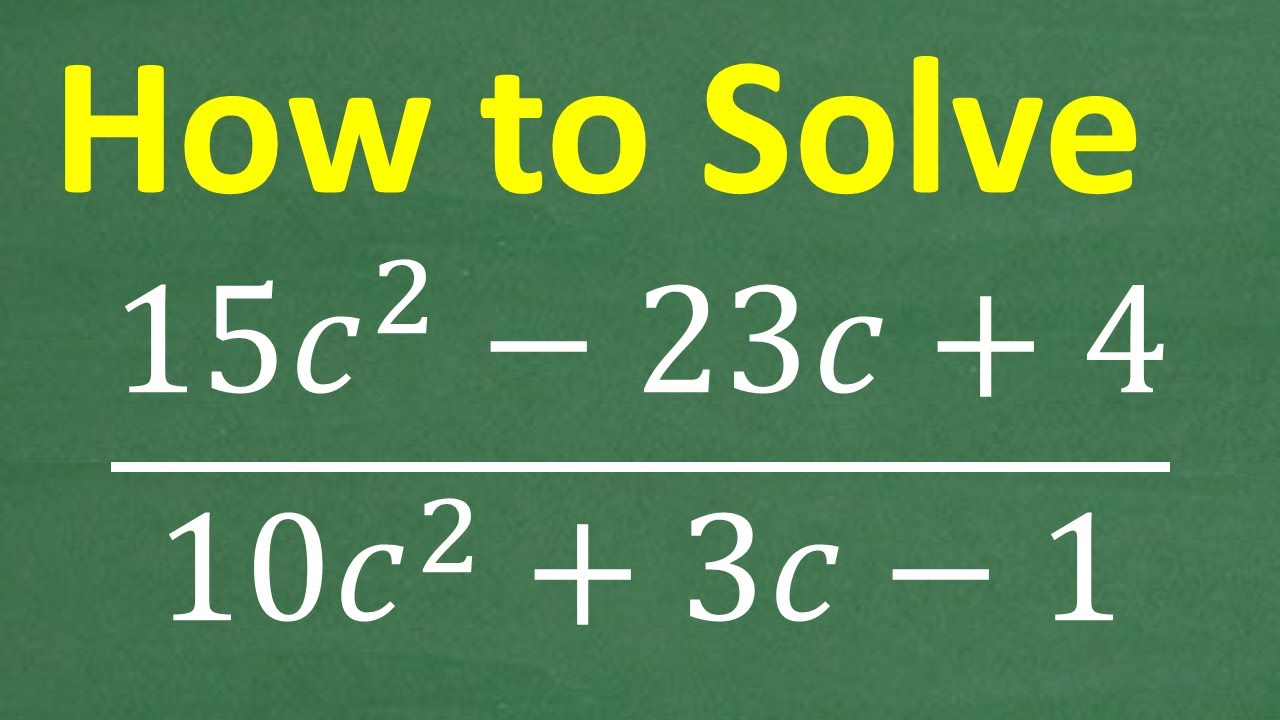
Показать описание
Help with Middle and High School Math
Test Prep for High School Math, College Math, Teacher Certification Math and More!
Popular Math Courses:
Math Foundations
Math Skills Rebuilder Course:
Pre-Algebra
Algebra
Geometry
Algebra 2
Pre-Calculus
• MIDDLE & HIGH SCHOOL MATH
• HOMESCHOOL MATH
• COLLEGE MATH
• TEST PREP MATH
• TEACHER CERTIFICATION TEST MATH
Simplifying Rational Expressions
How to simplify a rational expression using factoring
Simplifying Rational Expressions... How? (NancyPi)
Simplifying rational expressions introduction | Algebra II | Khan Academy
Simplify a rational expression
Simplifying Rational Algebraic Expression - Made Easy
How to Master Simplifying Rational Algebraic Expressions?
06 - Simplifying Rational Expressions in Algebra, Part 1
Simplification | BODMAS | Rules & Concepts Clarification | by NK Sir
Simplify the RATIONAL Expressions – how well can you factor?
Simplify a rational expression
Simplifying rational expression
Simplifying Complex Rational Expressions
MCR3U - Simplifying Rational Expressions Part 1 - Grade 11 Functions
Simplifying Rational expressions
Rational Expressions - Basic Introduction
How to Simplify Rational Algebraic Expressions?
Simplify rational expression using the rules of exponents
Simplify the rational expression and determine the excluded values
Simplifying a rational expression by factoring
Adding and Subtracting Rational Expressions With Unlike Denominators
Simplifying a complex rational expression
Manipulating Rational Expressions: Simplification and Operations
Simplifying Rational Algebraic Expressions (RAE) - Grade 8 Math
Комментарии
 0:11:08
0:11:08
 0:01:30
0:01:30
 0:14:04
0:14:04
 0:07:28
0:07:28
 0:07:47
0:07:47
 0:07:00
0:07:00
 0:08:27
0:08:27
 0:37:43
0:37:43
 0:03:54
0:03:54
 0:17:05
0:17:05
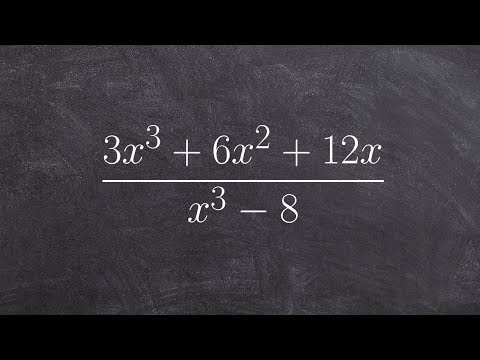 0:03:53
0:03:53
 0:02:38
0:02:38
 0:12:46
0:12:46
 0:07:54
0:07:54
 0:03:29
0:03:29
 0:12:46
0:12:46
 0:09:19
0:09:19
 0:07:50
0:07:50
 0:01:58
0:01:58
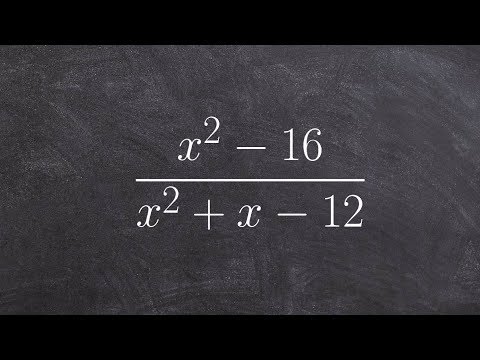 0:03:07
0:03:07
 0:13:14
0:13:14
 0:02:55
0:02:55
 0:09:30
0:09:30
 0:08:33
0:08:33