filmov
tv
Graphing Conic Sections Part 2: Ellipses

Показать описание
The next conic section is like a circle, but it's like someone stretched a circle out in a particular direction. It's the ellipse! These are very important in astronomy as most celestial objects follow elliptical paths. Let's learn all about ellipses and how to graph them.
Check out "Is This Wi-Fi Organic?", my book on disarming pseudoscience!
Check out "Is This Wi-Fi Organic?", my book on disarming pseudoscience!
Graphing Conic Sections Part 2: Ellipses
Graphing Conic Sections Part 3: Parabolas in Standard Form
Graphing Conic Sections Using Polar Equations - Part 2
Conic Sections: Graphing Ellipses Part 2
Graphing Conic Sections Part 1: Circles
Conic Sections Part 2 - Ellipse and Hyperbola
Writing Equations of Ellipses In Standard Form and Graphing Ellipses - Conic Sections
Conic Sections pt 2 - The Ellipse
Finding The Focus and Directrix of a Parabola - Conic Sections
Conic Sections: The Ellipse part 2 of 2
Conic Sections: Hyperbolas, Ellipses, Parabolas, Circles (How to Graph)
01 - Conic Sections: Ellipses - Graphing, Equation of an Ellipse, Focus - Part 1
Graphing Conic Sections Part 4: Hyperbolas
Hyperbolas - Conic Sections
13 - Conic Sections: Parabola, Focus, Directrix, Vertex & Graphing - Part 1
Conic Sections: The Ellipse - Part 2
Secret of solving and graphing Conic Sections Part II Hyperbola and Parabola
Conic Sections: Graphing Ellipses Part 1
Conic Sections #2 - Introduction to Graphing
Conic Sections Ellipses PT 2
Conic Sections: Parabolas, Part 2 (Directrix and Focus)
Conic Sections: The Parabola part 2 of 2
11.2 Equations and Graphs of Conic Sections - Circle and Ellipse
Conic Sections - Circles (Part 2 of 2)
Комментарии
 0:06:33
0:06:33
 0:08:30
0:08:30
 0:08:38
0:08:38
 0:13:37
0:13:37
 0:07:46
0:07:46
 0:11:18
0:11:18
 0:31:39
0:31:39
 0:23:31
0:23:31
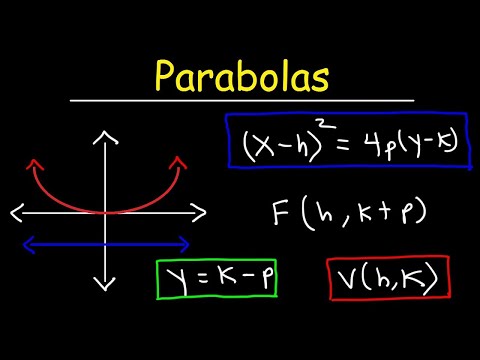 0:34:54
0:34:54
 0:10:00
0:10:00
 0:29:17
0:29:17
 0:33:42
0:33:42
 0:05:57
0:05:57
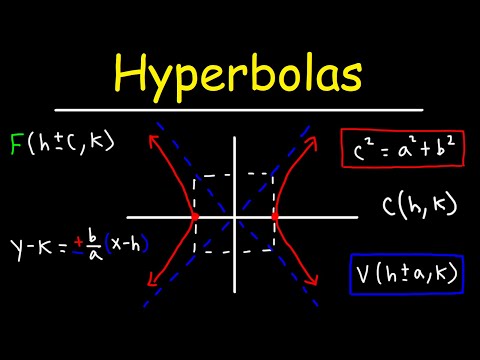 0:34:50
0:34:50
 1:00:16
1:00:16
 0:11:29
0:11:29
 0:39:27
0:39:27
 0:10:09
0:10:09
 0:21:08
0:21:08
 0:05:09
0:05:09
 0:07:27
0:07:27
 0:08:12
0:08:12
 0:21:05
0:21:05
 0:21:17
0:21:17