filmov
tv
Cross product: Proof determinant equals area of parallelogram
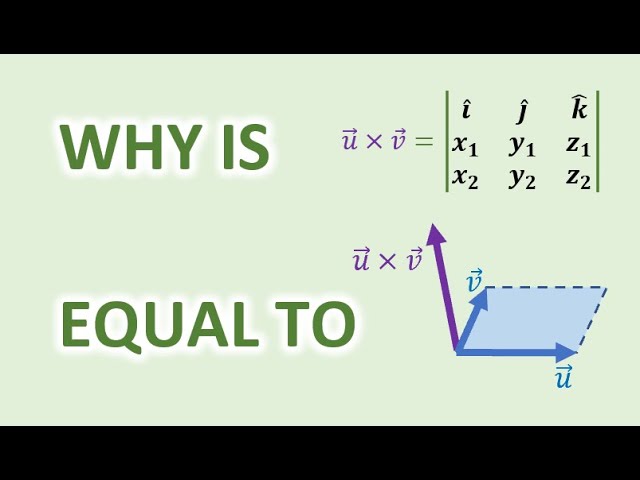
Показать описание
In the cross product u x v, if it's defined as a determinant, then it is not obvious why the length of u x v should equal the area of the parallelogram between them. This video presents a clever but simple proof.
Cross product: Proof determinant equals area of parallelogram
Cross products | Chapter 10, Essence of linear algebra
Cross Product #1 Explanation and Justification - FLT Proof #4.1.2.3
The connection between the cross product and the determinant
The Vector Cross Product
Cross Product - Vector Product - How to Derive the Formula - Determinant Method
Cross Product Derivation
Cross Product related to the Determinant
Graded sums on Dot product and cross product of vectors for class XII Mathematics
Cross Product #2 Explanation and Justification - FLT Proof #4.1.2.3
Determinant formula for the vector cross product
Why is the cross product PERPENDICULAR to both vectors?
The Cross Product in Determinant Form
Cross Product Derivation
Cross Product of Two Vectors Explained!
4: Cross Product - Valuable Vector Calculus
Cross products in the light of linear transformations | Chapter 11, Essence of linear algebra
The Length of a Cross Product: Proof
NYC - 5.6 - Cross Product Is Zero if and only if The Vectors are Parallel
4.5: Proof the Cross Product is Distributive - Valuable Vector Calculus
CalcBLUE 1 : Ch. 17.2 : Determinants and Cross Products
Linear Algebra 14TBD: The Product Property of the Determinant - Proof for Elementary Matrices
Cross Product Formula - What is CORRECT Sin Φ or Sin (360-Φ )?
Cross Product Proof
Комментарии
 0:06:59
0:06:59
 0:08:54
0:08:54
 0:19:23
0:19:23
 0:06:31
0:06:31
 0:06:46
0:06:46
 0:08:21
0:08:21
 0:32:55
0:32:55
 0:07:26
0:07:26
 1:02:30
1:02:30
 0:27:20
0:27:20
 0:00:47
0:00:47
 0:06:09
0:06:09
 0:18:49
0:18:49
 0:14:46
0:14:46
 0:13:47
0:13:47
 0:12:05
0:12:05
 0:13:10
0:13:10
 0:26:49
0:26:49
 0:16:28
0:16:28
 0:08:47
0:08:47
 0:03:30
0:03:30
 0:04:19
0:04:19
 0:00:32
0:00:32
 0:23:14
0:23:14