Example: Using Green's Theorem to Compute Circulation & Flux // Vector Calculus

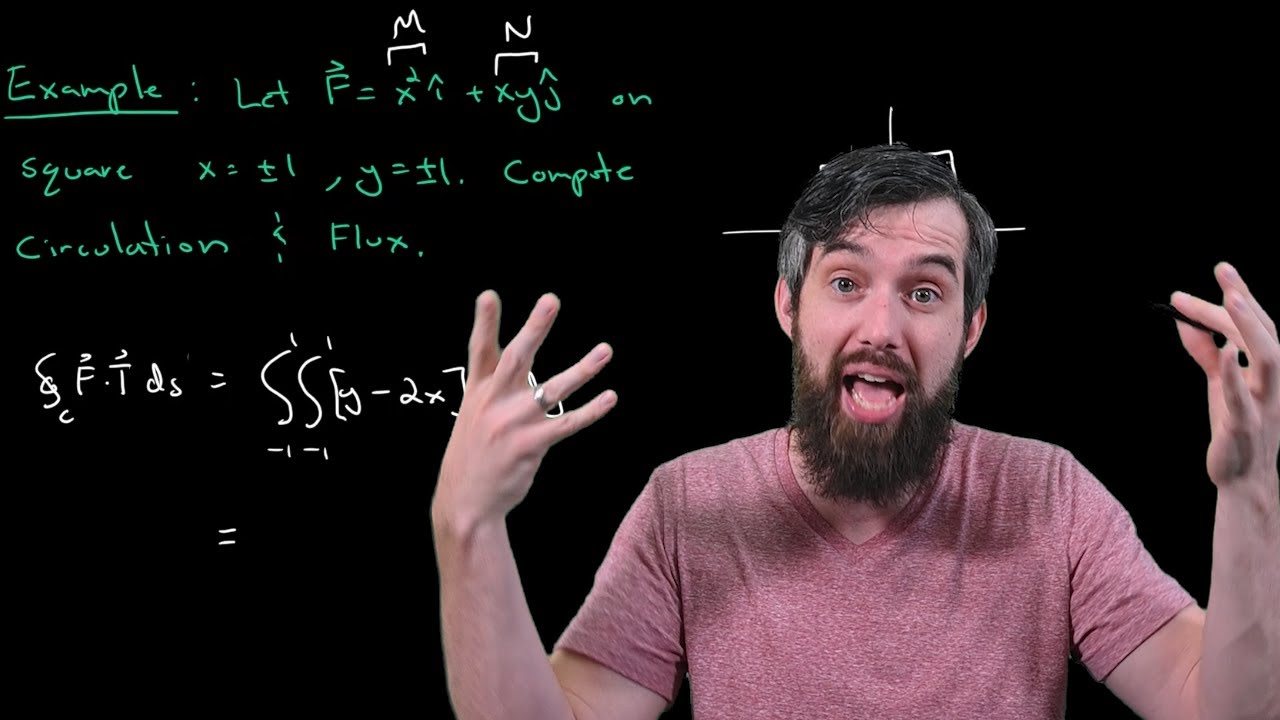
Показать описание

This video contains a pair of examples where we compute the Circulation (or Flow) of a vector field around a closed curve, and then again for the Flux. But we don't do it using line integrals, we use Green's Theorem parts I and II respectively to do the computation. This let's us compute a double integral over a region of either the circulation density (aka curl) or flux density (aka divergence) respectively. In the case of a square which is relatively easy to compute the double integral for, this is a significant advantage. Check out the previous videos in the vector calculus playlist for the geometric motivation of Green's Theorem.

0:00 Green's Theorem
1:28 Circulation Example
3:49 TYPO! Should substract partial M wrt y, not x.
4:00 Example continued
5:50 Flux Example

MY VECTOR CALCULUS PLAYLIST:

OTHER COURSE PLAYLISTS:

OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:

BECOME A MEMBER:

MATH BOOKS & MERCH I LOVE:

SOCIALS:

Рекомендации по теме

Комментарии

Welldone prof, quick one: please check 4:00. We ought to calculate dN/dx — dM/dy here, but dN/dx —dM/dx was computed. Thank you.

But funny enough, if this is followed, we both arrive at integral(2y. dy) = 0.

ogunsadebenjaminadeiyin

I think there is a typo at 3:54. You're supposed to subtract partial derivative of M with respect to y ( not x). So it's should be y -0 (not y-2x)

HungDuong-dtlg

I have been binge watching this playlist as I study the material for my final exam on calc3 in 5 days. Grasping the concepts visually thanks to you so Thank you so much Doctor! Liking all the videos too hehe.

alans

It's a good habit to upvote a high-quality youtube video so that more people could see it

proudaojiao

YOU TOO BETTER THAN OUR PROFESSORS. THANK YOU SO MUCH!!

rezwanaroza

Oh man… you are just excellent at teaching this topic. I am so grateful for these fantastic vids! Keep up the good work please!

fredericoamigo

"Big picture" of why both answers compute to zero: The field is symmetric about the origin in both its components. The M component has reflective symmetry, and the Y component has rotational symmetry. Since the region being evaluated (the square) is also symmetric about the origin, the net influence of the field on the region will be zero. If you translate the square in any direction, you'll get nonzero answers.

Stobber

2:16 ok thank you, that's what i need help with, the actual (in this case) four curves using the flux. Very difficult finding examples of this. But thank you for being upfront about it :)

EmpyreanLightASMR

I was struggling a lot to get the concepts of green's / stokes and divergence theorems. Thank you so much for uploading such a quality content. You a great teacher and explainer. Salutations. 🙏🙏

VijayPrajapati

Thank you sir for uploading such beautiful videos. Please upload more videos. I am a huge fan of your teaching!!! Always seeking your blessings Sir

hellocomputer

Good point. When calculating dM/dy, the integrand becomes ydxdy instead of (y-2x)dxdy; however, the final result remains the same: zero.

jgregory

Great series! Might be a better idea to compute curl and div on the vector fields you used to motivate Green's theorem. For curl, you could compute it on a field which goes counterclockwise and yields a non-zero curl value, and then on a field that just goes from left to right and has a zero curl. And then do the same for div: on vector fields that one can draw easily . I think its de-motivating to do only do examples where the curl and/or div end up being zero!

atomicgeneral

see and love your vidio from Kolkata, India.... i wish if you are my teacher 😄😄😄✌✌✌🤗🤗🤗🤗👍🏻👍🏻👍🏻

chuichi

thank you Sir... i enjoy learning math with your teaching

sureshpatel-sgxw

Curve convenient to evaluate the line integral, do so - region more complex, use Green's theorem - simple but brilliant nevertheless!

markpadley

Green was an amazing mathematician who didn't get discovered until when? After his death! Damn it! What a brilliant soul. He was self taught too. ugh! He is LEGENDARY!

guitarttimman

Sir I have a doubt ....in(3.46)
Sir it's the partial of M with respect to y but you took partial of M with respect to x ..why sir ..

kshitishp

The field F and the curve in this case is actually sysmetric. So if you stare at the four piece of the line integral long enough, you can see it should be zero for both circulation and flux :D

zhenlanwang

how can i join to this channel to be able to watch the following videos of this playlist

nkhheisenberg

Isnt there a problem that on the corners of the square there is no derivation and so the curve is not smooth and thus Greens theorem cant be used?

cloney

Example: Using Green's Theorem to Compute Circulation & Flux // Vector Calculus

Example: Using Green's Theorem to Compute Circulation & Flux // Vector Calculus

Green's Theorem

Green's theorem example 1 | Multivariable Calculus | Khan Academy

Ex: Use Green's Theorem to Evaluate a Line Integral (Polar)

Calculus 3: Green's Theorem (21 of 21) More Examples 4

Ex: Use Green's Theorem to Evaluate a Line Integral (Rectangle)

Green's Theorem, explained visually

Applying Greens Theorem, Superquiz 3 Problem 11

Vector integration Green's theorem best & easy example(PART-1)

Green's Theorem Examples

An Example Using Green’s Theorem

Green's Theorem

Green's functions: the genius way to solve DEs

Green's Theorem Example 1

Ex Use Green's Theorem to Evaluate a Line Integral Polar - Vector Calculus

Examples Using Green's Theorem

Green's Theorem #calculus #vectorcalculus

Multivariable Calculus - Using Green’s Theorem

Green's theorem example 2 | Multivariable Calculus | Khan Academy

How to use GREEN'S THEOREM and EXAMPLE

Green's theorem example | Vector Calculus | LetThereBeMath |

Using Greens Theorem

Ex: Use Green's Theorem to Determine Area of a Region Enclosed by a Curve

Ex: Use Green's Theorem to Evaluate a Line Integral (Negative Orientation)