filmov
tv
How To Solve Second Order Linear Homogeneous Differential Equation
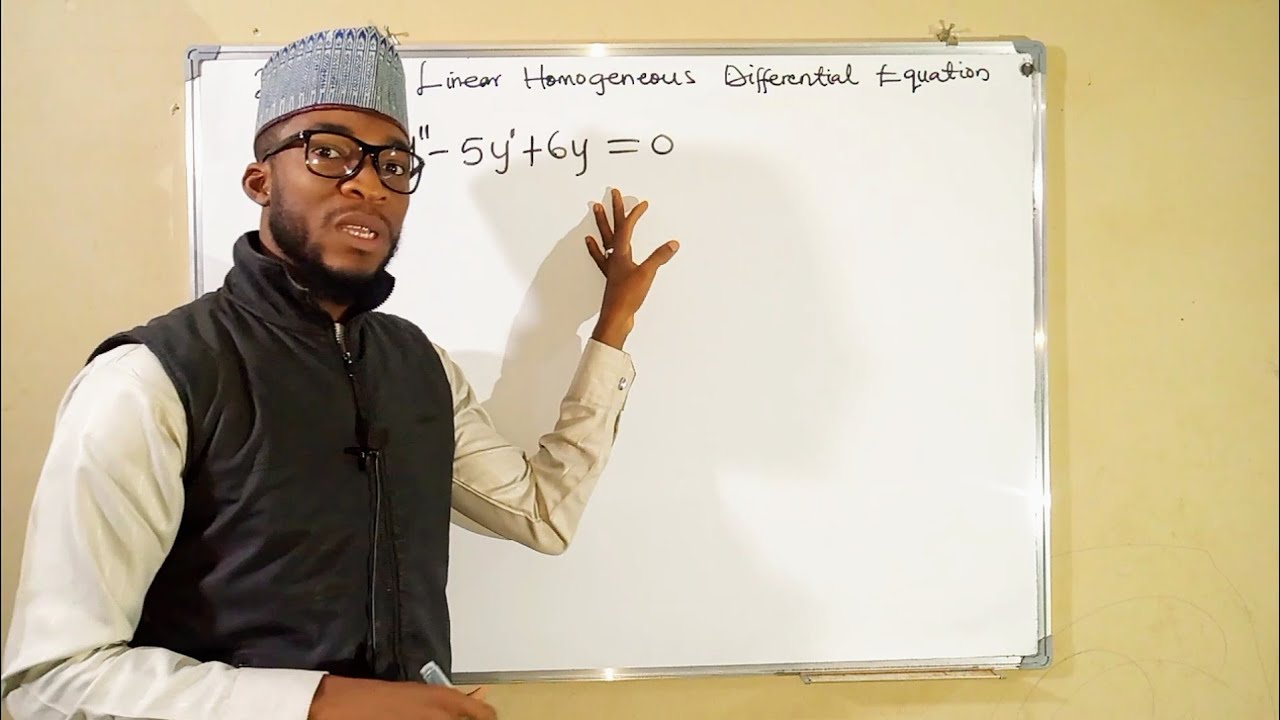
Показать описание
To solve any Second Order Linear Homogeneous Differential Equation, first this you need to do, is to transform the equation in to an auxiliary or characteristics equation in the form: ar²+be+c=0
We have already seen how to do that in our previous lesson.
The next move is to solve for r which are the roots of the equation (r intercept).
Then determine the nature of the roots and substitute in to the following equations, depending on the nature of roots.
y=C₁eʳ¹ˣ+C₂eʳ²ˣ. when you obtain real and distinct roots
y=(C₁+C₂x)eʳˣ when you Obtain real and equal roots.
and finally, if you Obtain a complex solution in the form: r= m+si or r = m-si
where i is imaginary number, and m and s are real numbers, then
y=eᵐˣ[C₁cos(st)+C₂sin(st)]
We have already seen how to do that in our previous lesson.
The next move is to solve for r which are the roots of the equation (r intercept).
Then determine the nature of the roots and substitute in to the following equations, depending on the nature of roots.
y=C₁eʳ¹ˣ+C₂eʳ²ˣ. when you obtain real and distinct roots
y=(C₁+C₂x)eʳˣ when you Obtain real and equal roots.
and finally, if you Obtain a complex solution in the form: r= m+si or r = m-si
where i is imaginary number, and m and s are real numbers, then
y=eᵐˣ[C₁cos(st)+C₂sin(st)]
0:25:17
Second Order Linear Differential Equations
0:32:54
Solving Second Order Differential Equations
0:06:41
How to Solve Constant Coefficient Homogeneous Differential Equations
0:12:44
Undetermined Coefficients: Solving non-homogeneous ODEs
0:03:02
How To Solve Second Order Linear Homogeneous Differential Equation
0:41:00
How to solve second order differential equations
0:11:44
Second order homogeneous linear differential equations with constant coefficients
0:04:35
Homogeneous Second Order Linear Differential Equations
0:41:28
Method of Undetermined Coefficients - Nonhomogeneous 2nd Order Differential Equations
0:11:19
The Theory of 2nd Order ODEs // Existence & Uniqueness, Superposition, & Linear Independence
0:25:18
Solving Non-Homogenous Second Order Differential Equations
0:05:08
How To Solve Second Order Linear Homogeneous Differential Equation | Involving Complex Roots
0:02:26
Learn How to Solve a Second Order Homogeneous Differential Equation with Distinct Real Roots
1:19:11
4. Second-Order Equations
0:14:29
Reduction of orders, 2nd order differential equations with variable coefficients
0:18:26
How to solve second order PDE
0:27:34
Analysis of Second Order Circuits
0:47:14
Reducible Second Order Differential Equations, Missing Y (Differential Equations 26)
0:07:08
Second order linear differential equation initial value problem , Sect 4.3 #21
0:03:51
Convert Second-order ODE to First-order Linear System
0:15:14
How To Solve Second Order Differential Equations Using Laplace Transform
0:17:39
Solving second order differential equation using operator D
0:07:47
Solve second order differential equation by substitution, Q10 on review sheet
0:04:16
Writing a second order differential equation as a system of first order equations.
Комментарии