Introduction to the Continuous Uniform Distribution

preview_player
Показать описание
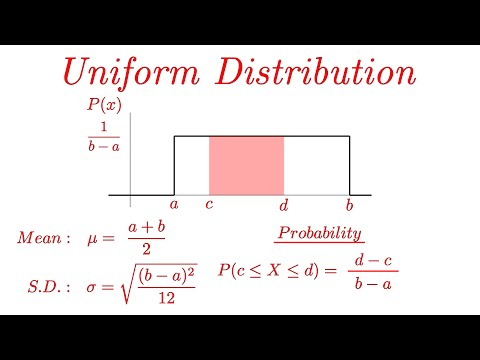
A brief introduction to the (continuous) uniform distribution. I discuss its pdf, median, mean, and variance. I also work through an example of finding a probability and a percentile. I don't do any integration in this video.

For those using R, here is the R code to find the probabilities for the examples in this video:

P(X greater than 230) where X is U(200,250):
1-punif(230,200,250)
[1] 0.4
(punif yields the area to the *left*, and here we need the area to the *right*)

20th percentile of a U(200,250) distribution:
qunif(.2,200,250)
[1] 210
  1. jbstatistics
  2. uniform distribution
  3. continuous uniform
  4. mean
  5. median
  6. variance
Рекомендации по теме
An Introduction to 0:06:57

An Introduction to the Continuous Uniform Distribution

Introduction to the 0:07:03

Introduction to the Continuous Uniform Distribution

Continuous Probability Uniform 0:31:26

Continuous Probability Uniform Distribution Problems

Uniform Distribution EXPLAINED 0:06:05

Uniform Distribution EXPLAINED with Examples

Introduction to the 0:20:57

Introduction to the Continuous Uniform Distribution

Continuous Probability Distributions 0:10:13

Continuous Probability Distributions - Basic Introduction

Continuous probability distribution 0:09:58

Continuous probability distribution intro

Continuous Uniform Distribution 0:10:30

Continuous Uniform Distribution (Intro)

Probability Distributions | 0:10:48

Probability Distributions | Random Variables | Continuous Random Variables | Graph of the CDF | 44 |

Introduction to Continuous 0:06:18

Introduction to Continuous Uniform Distribution#1

Introduction to Continuous 0:05:30

Introduction to Continuous Random Variables and the Uniform Distribution: Application

The Continuous Uniform 0:09:41

The Continuous Uniform Distribution and Integrals

An Introduction to 0:05:52

An Introduction to Continuous Probability Distributions

The Continuous Uniform 0:14:23

The Continuous Uniform Distribution

Introduction to Continuous 0:09:27

Introduction to Continuous Random Variables and the Uniform Distribution: Concept

S2 Edexcel Continuous 0:11:13

S2 Edexcel Continuous Uniform Distribution Introduction

Introduction to Mathematical 0:03:02

Introduction to Mathematical Statistics: Specific probability distributions (continuous uniform)

The Continuous Uniform 0:16:24

The Continuous Uniform Distribution

Introduction to continuous 0:11:53

Introduction to continuous probability distribution: Uniform distribution

Continuous Uniform Distribution 0:11:54

Continuous Uniform Distribution Example and Concept

S2 4.1 Continuous 0:11:16

S2 4.1 Continuous uniform distribution

The Continuous Uniform 0:14:49

The Continuous Uniform and Normal Distributions

Introduction to Discrete 0:02:26

Introduction to Discrete Uniform Distribution

A Simply-introduction to 0:02:24

A Simply-introduction to the Continuous Uniform Distribution

Комментарии
Автор

Some sources have the boundaries included, some not. Unless we're getting very technical, it doesn't matter whether we say f(x) = 1/(d-c) for c < x < d, or c < = x < = d. The cumulative distribution function F(x) = P(X <=x ) will be 0 for x < = c in either case, and F(x) = 1 for x greater or equal to d in either case as well. Whether the boundaries are included or not doesn't change anything, other than very technical details that are far beyond my treatment of this topic.

jbstatistics
Автор

great video man i've been missing my lectures this is helpful

mistathugisolation
Автор

Hi I have a question for the discussion at 1:45. I thaught that f(x)=0 if x is greater than or equal to c. and f(x)=1 if x is greater than or equal to d. So I thaught that f(x) can only to equal to 1/d-c if x is greater than c (not equal to) and less than d (not equal to). Have I misunderstood this?

mickysahi