filmov
tv
Thin-Walled PRESSURE VESSELS in 8 MINUTES - Mechanics of Materials
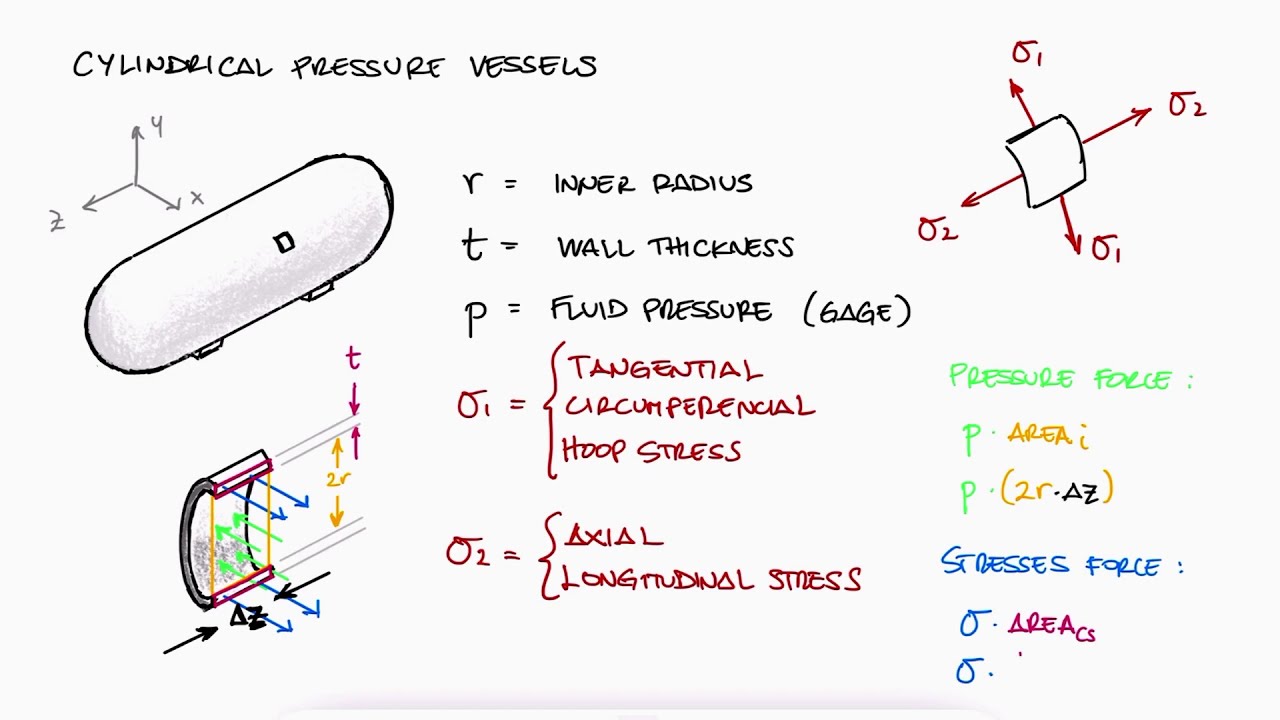
Показать описание
Hoop Stress (tangential, circumferential), Longitudinal Stress (axial), and more!
0:00 Pressure Vessels Stresses
0:40 Dimensions Nomenclature
0:59 Hoop Stress (Cylindrical)
2:02 Longitudinal Stress
2:48 Spherical Vessel Stresses
3:50 Principal Stresses
4:14 Cylindrical Principal Stresses
5:28 Spherical Principal Stresses
6:33 Pressure Vessel Example
__________________________________________________________
Previous Main Video Link:
Principal Stresses and MOHR'S CIRCLE in 12 Minutes!!
Next Main Video Link:
Yield (DUCTILE) Failure Theories in Just Over 10 Minutes!
______________________________________________________________
Other Mechanics of Materials Lectures:
Watch the entire course in less than 4 HOURS!!
20 Elastoplastic Beams and Residual Stresses (torsion too): coming soon
0:00 Pressure Vessels Stresses
0:40 Dimensions Nomenclature
0:59 Hoop Stress (Cylindrical)
2:02 Longitudinal Stress
2:48 Spherical Vessel Stresses
3:50 Principal Stresses
4:14 Cylindrical Principal Stresses
5:28 Spherical Principal Stresses
6:33 Pressure Vessel Example
__________________________________________________________
Previous Main Video Link:
Principal Stresses and MOHR'S CIRCLE in 12 Minutes!!
Next Main Video Link:
Yield (DUCTILE) Failure Theories in Just Over 10 Minutes!
______________________________________________________________
Other Mechanics of Materials Lectures:
Watch the entire course in less than 4 HOURS!!
20 Elastoplastic Beams and Residual Stresses (torsion too): coming soon
Thin-Walled PRESSURE VESSELS in 8 MINUTES - Mechanics of Materials
Mechanics of Materials: Lesson 41 - Intro to Thin Walled Pressure Vessels
[A55] MEC 32 Lesson 6: Thin-walled Pressure Vessels (1/3)
CYLINDRICAL Pressure Vessel Stresses in Under 2 Minutes!
07.1 Thin walled pressure vessels
Thin Wall Pressure Vessel 2.MP4
Thin-Walled Pressure Vessels
The Aluminum Beverage Can - Thin Walled Pressure Vessel
Understanding The Basics of Thin-Walled Pressure Vessels
Mechanics of Materials: Lesson 42 - Thin Walled Pressure Vessel Example Problem
Thin Walled Pressure Vessel – Part 2 (Data Acquisition).
Lecture 8a thick and thin walled pressure vessels
Materials Science Thin Walled Cylindrical Pressure Vessels
SPHERICAL Pressure Vessel in Under 2 Minutes!
Thin Walled Pressure Vessel Problem: Stress and Strain Tensors In A Copper Pipe
Mechanics of Materials | Thin walled Pressure Vessels | Solved Example 5| Filament wound PV
(20AA) Thin-walled pressure vessels
Statics and Mechanics | Thin-Wall Pressure Vessels
thin-walled pressure vessels example
Lecture 9: Thin Walled Pressure Vessel Strain Gauge Shunt Calibration Example Problem
Maximum Internal Pressure in Cylindrical PRESSURE VESSEL in 80 Seconds!
ENGR 216 Lecture 22: Comb. Loading [cont'd] & Thin-Walled Pressure Vessels (2016.11.15)
Mechanics of Materials | Thin walled Pressure Vessels | Solved Example 3
Module 4: Hoop Stress - Mechanics of Materials II: Thin-Walled Pressure Vessels and Torsion
Комментарии
 0:08:17
0:08:17
 0:09:31
0:09:31
![[A55] MEC 32](https://i.ytimg.com/vi/oXst7O7Gh9A/hqdefault.jpg) 0:16:01
0:16:01
 0:01:35
0:01:35
 0:08:39
0:08:39
 0:09:41
0:09:41
 0:07:38
0:07:38
 0:02:15
0:02:15
 0:04:03
0:04:03
 0:11:10
0:11:10
 0:04:33
0:04:33
 0:02:45
0:02:45
 0:09:51
0:09:51
 0:01:36
0:01:36
 0:11:09
0:11:09
 0:11:52
0:11:52
 0:08:07
0:08:07
 0:48:11
0:48:11
 0:03:14
0:03:14
 0:10:17
0:10:17
 0:01:21
0:01:21
 1:00:43
1:00:43
 0:09:16
0:09:16
 0:03:03
0:03:03