filmov
tv
Line integral example from Vector Calculus
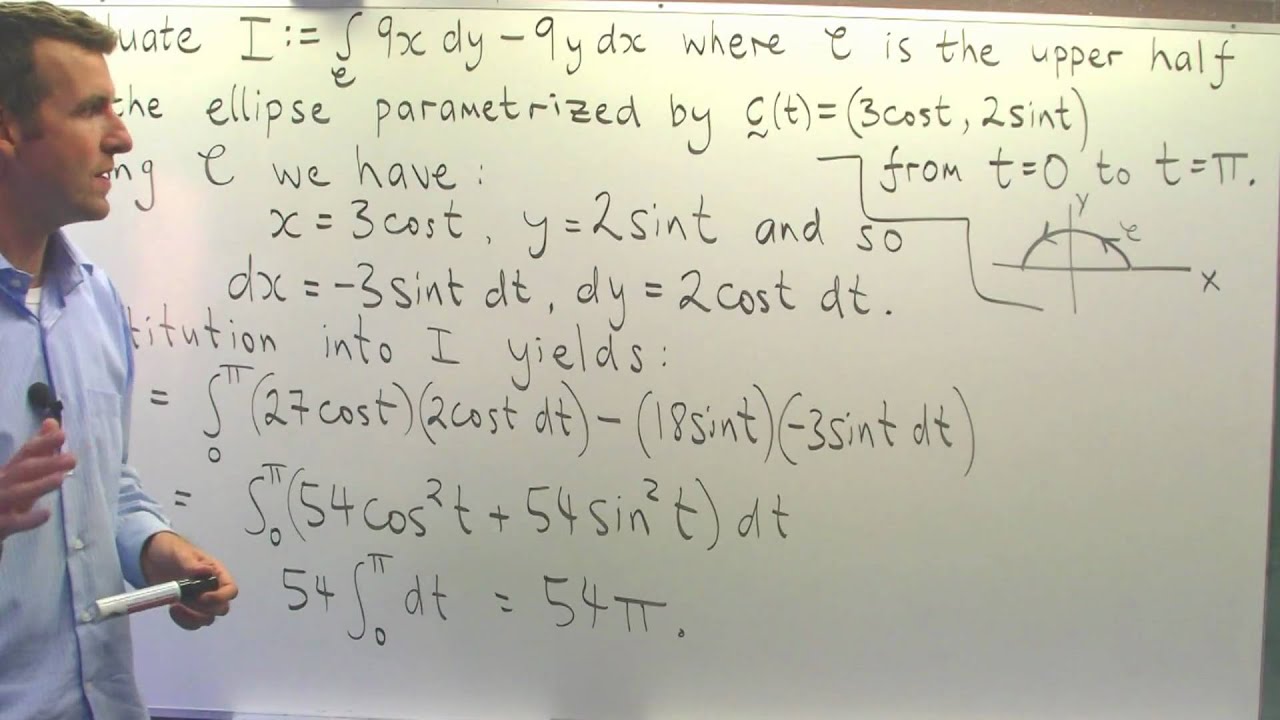
Показать описание
I discuss and solve a simple problem that involves the evaluation of a line integral. This particular line integral is in the differential form. The method used to solve this problem is one that involves a simple substitution. Such an example is seen in 2nd-year university mathematics.
How to Evaluate the Line Integral of a Vector Field
line integral of a vector function (KristaKingMath)
Line integral example from Vector Calculus
Line Integrals of Vector Fields Practice Problems
Calculus 3: Line Integrals (18 of 44) What is a Line Integral? [(y)dx+(z)dy+(x)dz] Example 6
Multivariable Calculus | Vector line integral example
Example: Computing the Line Integral of a Vector Field (i.e. Work Done)
Physics Ch 67.1 Advanced E&M: Review Vectors (50 of 113) Line Integral Example 2 Path 1
parameterization of surface in calculus - area Jacobian |d(x, y) /d(u, v)| case study, polar part 14
Line integrals and vector fields | Multivariable Calculus | Khan Academy
Line Integrals of Vector Fields // Big Idea, Definition & Formula
Line integral example 1 | Line integrals and Green's theorem | Multivariable Calculus | Khan Ac...
Evaluating Line Integrals
Line Integral Example
Second example of line integral of conservative vector field | Multivariable Calculus | Khan Academy
Line Integrals Practice Problems
Line integral of a vector field
Line Integral Evaluation Example 1
Using a line integral to find the work done by a vector field example | Khan Academy
What is a LINE INTEGRAL? // Big Idea, Derivation & Formula
Line Integral of Vector Fields
Line Integrals in 3D // Formula & Three Applications
Beauty of Line Integral (Calculus) .
Fundamental Theorem for Line Integrals :: Conservative Vector Field Line Integral
Комментарии
 0:06:16
0:06:16
 0:10:39
0:10:39
 0:07:29
0:07:29
 0:09:02
0:09:02
 0:05:03
0:05:03
 0:02:56
0:02:56
 0:06:55
0:06:55
 0:07:01
0:07:01
 0:34:07
0:34:07
 0:16:47
0:16:47
 0:08:40
0:08:40
 0:13:03
0:13:03
 0:12:54
0:12:54
 0:07:39
0:07:39
 0:10:19
0:10:19
 0:13:00
0:13:00
 0:14:26
0:14:26
 0:08:34
0:08:34
 0:11:32
0:11:32
 0:14:02
0:14:02
 0:07:49
0:07:49
 0:05:49
0:05:49
 0:08:56
0:08:56
 0:08:09
0:08:09