Control Charts simply explained - Statistical process control - Xbar-R Chart, I-MR Chart,...

preview_player
Показать описание
In this video, we delve into the fundamentals of Control Charts (Statistical Process Control - SPC), a vital tool in quality control and process management. Learn how to monitor processes, detect variations, and maintain consistent quality over time.

We'll cover:
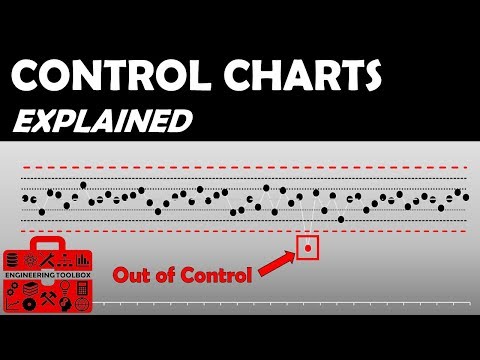
What Control Charts are and why they are essential.
Different types of Control Charts (Xbar-R Chart, I-MR Chart, p Chart, np Chart, c Chart and u Chart).
How to create and interpret Control Charts.
Real-world examples of using Control Charts in various industries.

► EBOOK

► Control Chart Calculator

0:00 What are Control Charts?
1:04 What is a Xbar-R Chart?
5:05 What is an I-MR Chart?
6:34 What is a np Chart and a p Chart?
9:08 What is a c Chart and a u Chart?
  1. DATAtab
Рекомендации по теме
Control Charts simply 0:11:04

Control Charts simply explained - Statistical process control - Xbar-R Chart, I-MR Chart,...

CONTROL CHART BASICS 0:12:16

CONTROL CHART BASICS and the X-BAR AND R CHART +++++ EXAMPLE

How do SPC 0:08:49

How do SPC control charts work?

SPC Control Charting 0:11:20

SPC Control Charting Rules

The 7 Quality 0:16:04

The 7 Quality Control (QC) Tools Explained with an Example!

Basics of Control 0:06:34

Basics of Control Charts

Introduction to Statistical 0:24:15

Introduction to Statistical Process Control Charts (Lean Six Sigma)

SPC - The 0:04:39

SPC - The Lean Six Sigma Tool You Must Know (Statistical Process Control)

How Institutions Control 0:12:46

How Institutions Control the Market: Smart Money Explained!

Control Chart Interpretation 0:06:27

Control Chart Interpretation

Run chart vs 0:04:17

Run chart vs control chart, Run chart explained, Control chart explained

Attribute Data Control 0:18:41

Attribute Data Control Chart Examples!! How to select/create the P, NP, C and U Charts

Using Control Charts 0:11:58

Using Control Charts

Introduction to Statistical 0:08:45

Introduction to Statistical Process Control Charts | Dr. Harper's Classroom

Making a Control 0:11:03

Making a Control Chart in Excel (with dynamic control lines!)

'Control Chart' with 0:06:39

'Control Chart' with Carsten Lützen

QC101 Control Charts 0:21:01

QC101 Control Charts

PMBOK 6. 8.2.5. 0:12:13

PMBOK 6. 8.2.5. Control Chart - PMP Exam

Six Sigma | 0:05:45

Six Sigma | Overview of the Control Chart | Green Belt 2.0® Lean Six Sigma | fkiQuality HD

Complexity Made Simple 0:07:05

Complexity Made Simple - Why Statistical Process Control (SPC)

Run Charts in 0:07:34

Run Charts in Quality Improvement

Create a Basic 0:15:14

Create a Basic Control Chart | HOW TO CREATE CONTROL CHARTS IN EXCEL | Shewhart Control Chart

What is a 0:19:23

What is a Control Chart? | Control Chart in Quality Control | Invensis Learning

Learn about Control 0:00:53

Learn about Control Charts in less than a minute #shorts #youtubeshorts #shortsvideo #shortvideo

Комментарии
Автор

That is so nice. Within 10 minutes, had an idea about various Control Charts. Thank you.

xlisgr
Автор

I have been in quality for over 30 years, and in my lifetime, only a few people have been able to explain it as nicely as you did.

Every time I mentored my colleagues, I tried to explain Control Chart methodology similarly to how you explained it.

Kudos!

haroldsimpson
Автор

Thank you so much for explaining this concept better ....

RendzoChabalala
Автор

Please explain about Six Sigma concept also with reference to statistical measures.

xlisgr
Автор

Thank you very much...Are these tests important in medical statistics?!

mohammedelbarbary
Автор

Hello, nice overvieuw video.
In the example of the XBarChart you take 25 data points (each containing 5 samples a day) so in fact the UCL/LCL are based on 5x 25 samples = 125 samples Yes?

But suppose in a laboratory certain analysis runs on one daily run with control standards/samples
... so 1 datapoint/day

1. How many samples (days) would you take to calculate the Mean, StdDev and UCL/LCL ?
Should you take 30 as a minimum (30 is the border between T-distr. vs. Normal distr.) or do you take another statistical limit ?

2. When, in time, there is a clear indication of a shift of the mean (up or down...) how to react in a correct way for recalculation of Mean, StdDev, UCL/LCL etc... ?

brudo