filmov
tv
Integral ln(sin x) from 0 to pi/2
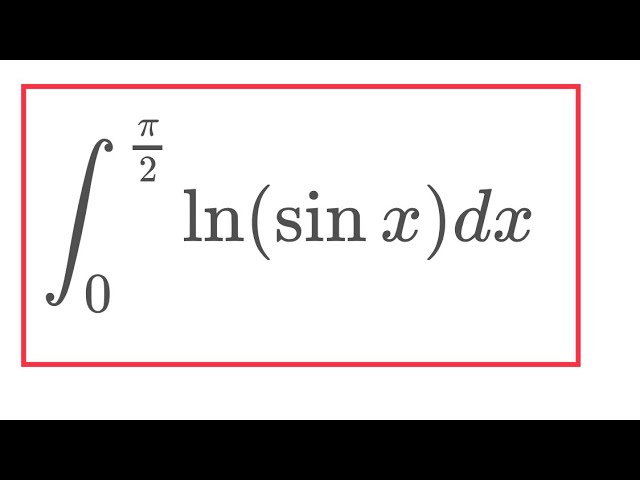
Показать описание
In this video, yet another Peyam Classic, I calculate the integral of ln(sin x) from 0 to pi/2 using a clever u-substitution. Thank you Zach Lee for giving me the main ideas for the proof!
Integral ln(sin x) from 0 to pi/2
Improper Integral of ln(sinx) from 0 to pi/2: MIT Integration Bee (4)
Integral of ln(sin x)
How to compute this integral? || ln(sin(x))
The Most Useful Integration Formula : ∫ ln(sinx)dx
Integral of ln(sinx) from 0 to pi/2
integration of ln(sinx) from 0 to phi/2
A crazy complex integral! - feat. Milo [ ln(cos(x))ln(sin(x))/tan(x) from 0 to pi/2 ]
Integral of ln(sin x) from 0 to pi/4
Integral of ln(sinx) from 0 to pi/3
Integrate ln(|sin x|) dx from 0 to pi/2
Integral of ln(sinx) from 0 to pi/2 | #Shorts
integral ln sinx from 0 to pi/2 | An interesting integral
Integral of ln(sinx) from 0 to pi/4
2. (Calculus) Definite Integral of f(x)=ln(sinx) from 0 to pi/2 (important example)
Why ∫ln(cos(x)) dx [0, π/2] = ∫ln(sin(x)) dx [0, π/2] = -ln(2)π/2 ??
Unlock the Secrets of ln(sin(x)) Differentiation (Quick & Efficient Method)
Integral of Sin(lnx)
Integral from 0 to pi/2 of (ln(cosx)ln(sinx))/(tanx)
Integral ln(sinx)ln(cosx)/tanx from 0 to pi/2
LES INTÉGRALES D'EULER (intégrale de ln(sin x))
Video 2034.23 - Integrate sinx ln(sinx)
integral of sin(ln(x)), integration by parts with u substitution
How to integrate cotx ln(sinx )dx
Комментарии
 0:13:37
0:13:37
 0:13:24
0:13:24
 0:09:52
0:09:52
 0:11:46
0:11:46
 0:07:01
0:07:01
 0:00:31
0:00:31
 0:04:25
0:04:25
 0:09:34
0:09:34
 0:23:03
0:23:03
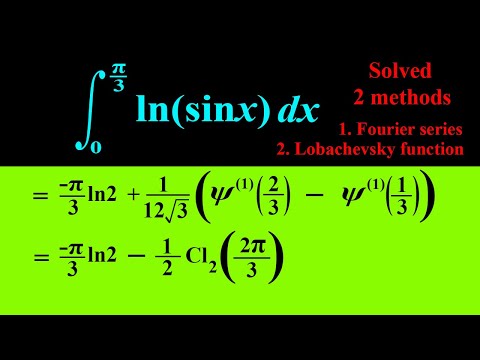 0:15:39
0:15:39
 0:03:21
0:03:21
 0:00:55
0:00:55
 0:08:32
0:08:32
 0:17:33
0:17:33
 0:14:42
0:14:42
 0:05:02
0:05:02
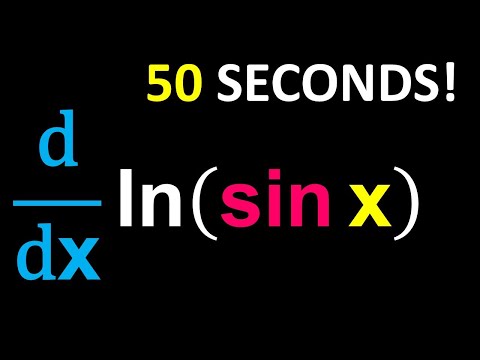 0:00:55
0:00:55
 0:08:25
0:08:25
 0:06:55
0:06:55
 0:07:38
0:07:38
 0:09:40
0:09:40
 0:02:46
0:02:46
 0:03:50
0:03:50
 0:03:14
0:03:14