Integral of ln(sinx) from 0 to pi/3

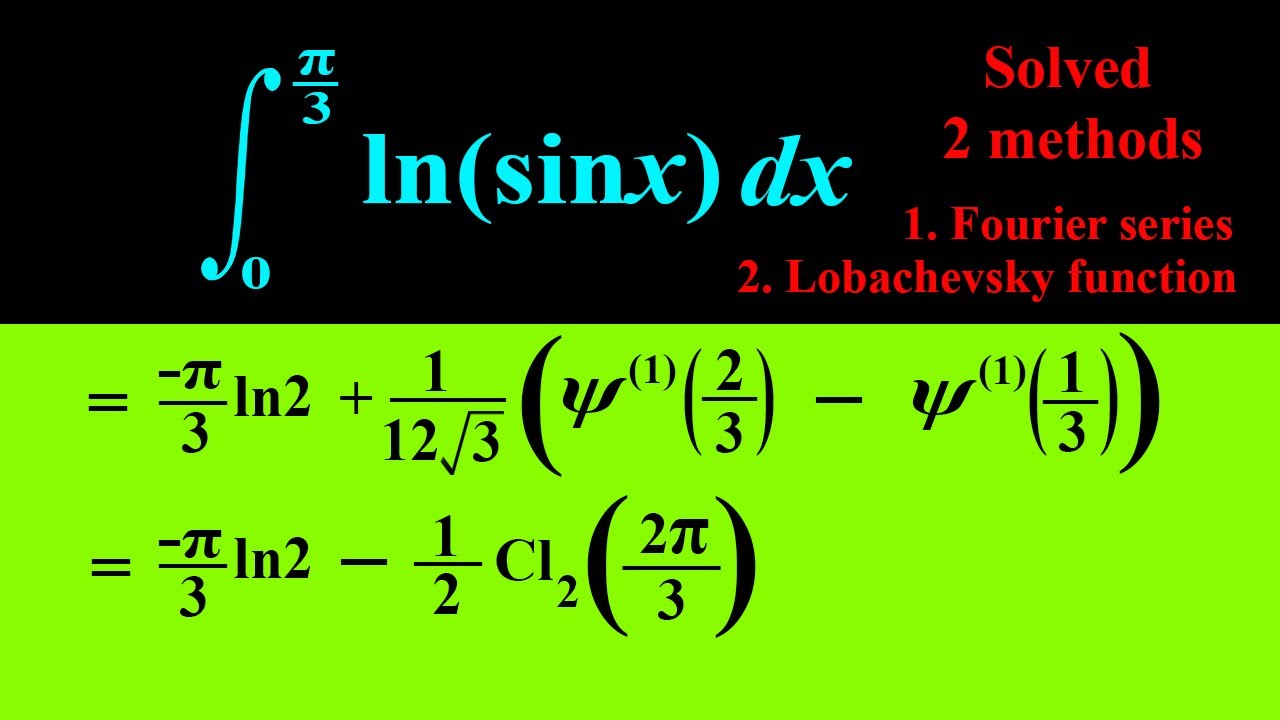
preview_player
Показать описание
Integral of ln(sinx) from 0 to pi/3, is a little bit hard integral to integrate, however In this video I evaluated it by using 2 different method. First I used Fourier series for ln(sinx) and second time I used Lobachevski function.
In previous videos I evaluate Integral ln(sinx) from 0 to pi/2 and integral ln(sinx) from 0 to pi/4 so, I thought to create a content for integrate Integral of ln(sinx) from 0 to pi/3.

Integration of lnsinx from 0 to pi/3 | Integration | ln(sinx) integral | Integrals | Hard Integral

#Integration #lnSinx #Math
  1. Mathematics MI
  2. integration of ln(sinx) from 0 to pi/3
  3. integration of ln sinx
  4. integration of ln sinx dx
  5. ln sinx
  6. ln sinx integral
Рекомендации по теме
integration of ln(sinx) 0:04:25

integration of ln(sinx) from 0 to phi/2

Integral of ln(sinx) 0:17:33

Integral of ln(sinx) from 0 to pi/4

Integral of ln(sinx) 0:15:39

Integral of ln(sinx) from 0 to pi/3

The Most Useful 0:07:01

The Most Useful Integration Formula : ∫ ln(sinx)dx

Improper Integral of 0:13:24

Improper Integral of ln(sinx) from 0 to pi/2: MIT Integration Bee (4)

Integral of ln(sinx) 0:00:31

Integral of ln(sinx) from 0 to pi/2

integral ln sinx 0:08:32

integral ln sinx from 0 to pi/2 | An interesting integral

Integral ln(sin x) 0:13:37

Integral ln(sin x) from 0 to pi/2

Integral from 0 0:06:55

Integral from 0 to pi/2 of (ln(cosx)ln(sinx))/(tanx)

Integral of ln(sinx) 0:00:55

Integral of ln(sinx) from 0 to pi/2 | #Shorts

Integral of ln(sin 0:09:52

Integral of ln(sin x)

2. (Calculus) Definite 0:14:42

2. (Calculus) Definite Integral of f(x)=ln(sinx) from 0 to pi/2 (important example)

Integral ln(sinx)ln(cosx)/tanx from 0:07:38

Integral ln(sinx)ln(cosx)/tanx from 0 to pi/2

Integrate ln(sinx) or 0:06:48

Integrate ln(sinx) or ln(cosx) from 0 to pai /2 | Definite Integral class-12 | Jee | Jee main

How to integrate 0:03:14

How to integrate cotx ln(sinx )dx

Video 2034.23 - 0:02:46

Video 2034.23 - Integrate sinx ln(sinx)

Derivative of ln[sinx], 0:00:22

Derivative of ln[sinx], 20 seconds

Integral of ln(x) 0:00:45

Integral of ln(x) fast!

Consider is `int_(0)^(pi//2) 0:02:57

Consider is `int_(0)^(pi//2) ln (sinx)dx` equal to ? What is `int_(0)^(pi//2)

Calculus Derivative of 0:04:31

Calculus Derivative of Functions with Natural Log ln (sinx)

How REAL Men 0:00:35

How REAL Men Integrate Functions

Integration of ln(sinx) 0:17:21

Integration of ln(sinx)

Consider is `int_(0)^(pi//2) 0:03:11

Consider is `int_(0)^(pi//2) ln (sinx)dx` equal to ? What is `int_(0)^(pi//2)ln (sinx) dx`

integration of ln(sinx) 0:17:52

integration of ln(sinx) when upper limit is pi/2 and lower limit is 0

Комментарии
Автор

This is amazing.... great great great job... first time I saw this in YouTube or any other social media.. also I couldn’t find this integral in any book...Thank you very much.. really appreciate.. ❤️

michellanderson
Автор

Another interesting one. Previous days I watch some of your videos. Amazing keep it up..Thank you

RadhaSharma-jwux
Автор

From fourier series to polygamma function, outstanding derived!

王天祥-ji
Автор

Great!
can you provide a reference relating trigamma function and clausen function?

carlosgiovanardi
Автор

Hey can't we use complex definition of sinx it will also a elegant solution

gopimaji
Автор

"Fourier series of ln(sin(x)) is equal to..." Where would we find this out? I have never thought of taking the Fourier series of the logarithm. I can see it's a periodic function, but I wouldn't know how to reduce it to a series.

zh