filmov
tv
Quantum chaos, random matrices and statistical physics (Lecture 04) by Arul Lakshminarayan
Показать описание
ORGANIZERS: Abhishek Dhar and Sanjib Sabhapandit
DATE: 27 June 2018 to 13 July 2018
VENUE: Ramanujan Lecture Hall, ICTS Bangalore
This advanced level school is the ninth in the series.
This is a pedagogical school, aimed at bridging the gap between masters-level courses and topics in statistical physics at the frontline of current research. It is intended for Ph.D. students, post-doctoral fellows and interested faculty members at the college and university level. The following courses will be offered.
Preparatory lecturers by Abhishek Dhar (ICTS) and Sanjib Sabhapandit (RRI)
Stochastic density functional theory for interacting Brownian particles by David Dean (Bordeaux, France)
Mechanics of wrinkling, folding, and crumpling by Narayanan Menon (UMASS, USA)
Network Dynamics by Sandeep Krishna (NCBS) and Shashi Thutupalli (NCBS-ICTS)
Quantum computation by Peter Young (UCSC, USA)
Quantum chaos, random matrices and statistical physics by Arul Lakshminarayan (IIT Madras, Chennai)
Interacting particle systems by Anupam Kundu (ICTS, Bangalore)
0:00:00 Bangalore School Statistical Physics - IX
0:00:10 Quantum chaos, random matrices and statistical physics (Lecture - 04)
0:00:35 Simple model of Quantum Chaos / Quantum maps
0:02:58 1.5 Degree of freedom
0:06:02 Standard Map
0:08:23 Diffusion in Momentum
0:27:02 Angular Momentum
0:30:58 Observations
0:38:42 Quantum Maps: Generalities
0:45:57 Quantum States
0:50:12 Example
0:57:17 Quantum Mechanics
0:57:55 Calculate the Eigen Functions
1:05:08 2.4 Eigenvalues and quantum chaos
1:09:16 Quantum chaos, RMT and statistical physics
1:12:25 Chapter 2: Hamiltonian Chaos Quantum Mechanics
1:13:08 Figure 2.9: Energy vs magnetic field for the H atom.
1:13:59 Figure 10: The spectral staircase function when the potential is simply x2 y2. From Tonsovic. J. Phys. A.1991
1:20:53 Figure 2.11: Refers to the Hamiltonian in Eq. (1.36) and to Fig. (1.3.2)
DATE: 27 June 2018 to 13 July 2018
VENUE: Ramanujan Lecture Hall, ICTS Bangalore
This advanced level school is the ninth in the series.
This is a pedagogical school, aimed at bridging the gap between masters-level courses and topics in statistical physics at the frontline of current research. It is intended for Ph.D. students, post-doctoral fellows and interested faculty members at the college and university level. The following courses will be offered.
Preparatory lecturers by Abhishek Dhar (ICTS) and Sanjib Sabhapandit (RRI)
Stochastic density functional theory for interacting Brownian particles by David Dean (Bordeaux, France)
Mechanics of wrinkling, folding, and crumpling by Narayanan Menon (UMASS, USA)
Network Dynamics by Sandeep Krishna (NCBS) and Shashi Thutupalli (NCBS-ICTS)
Quantum computation by Peter Young (UCSC, USA)
Quantum chaos, random matrices and statistical physics by Arul Lakshminarayan (IIT Madras, Chennai)
Interacting particle systems by Anupam Kundu (ICTS, Bangalore)
0:00:00 Bangalore School Statistical Physics - IX
0:00:10 Quantum chaos, random matrices and statistical physics (Lecture - 04)
0:00:35 Simple model of Quantum Chaos / Quantum maps
0:02:58 1.5 Degree of freedom
0:06:02 Standard Map
0:08:23 Diffusion in Momentum
0:27:02 Angular Momentum
0:30:58 Observations
0:38:42 Quantum Maps: Generalities
0:45:57 Quantum States
0:50:12 Example
0:57:17 Quantum Mechanics
0:57:55 Calculate the Eigen Functions
1:05:08 2.4 Eigenvalues and quantum chaos
1:09:16 Quantum chaos, RMT and statistical physics
1:12:25 Chapter 2: Hamiltonian Chaos Quantum Mechanics
1:13:08 Figure 2.9: Energy vs magnetic field for the H atom.
1:13:59 Figure 10: The spectral staircase function when the potential is simply x2 y2. From Tonsovic. J. Phys. A.1991
1:20:53 Figure 2.11: Refers to the Hamiltonian in Eq. (1.36) and to Fig. (1.3.2)
0:41:01
1:09:35
1:35:23
1:29:40
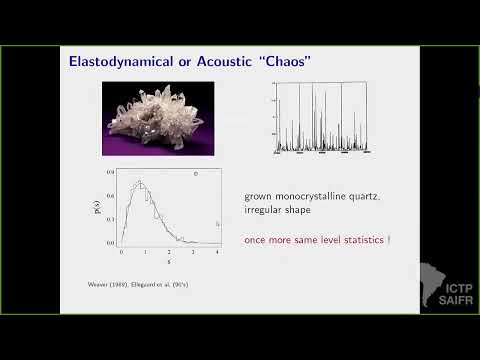1:31:25
0:39:19
1:42:23
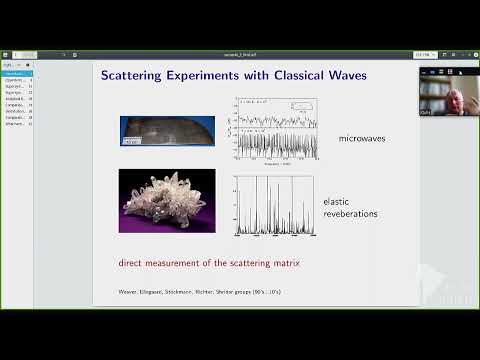1:39:12
1:28:39
0:50:46
1:12:36
0:53:53
1:10:07
1:03:19
1:38:36
1:26:32
0:59:47
0:01:26
0:32:21
1:14:47
1:20:51
0:59:11
1:10:05
1:06:16