Beautiful dodecagon dissection

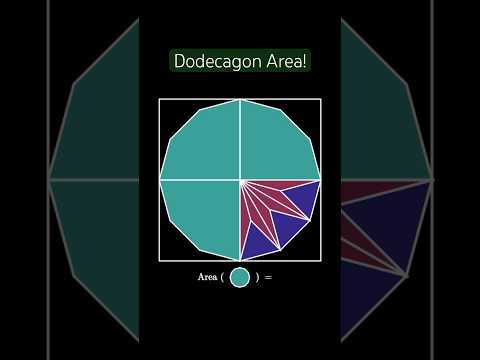
This is a short, animated visual proof demonstrating that the area of a regular dodecagon inscribed in the unit circle has an area of exactly 3.

This animation is based on a dissection by J. Kürschák that appears in the following sources:

Mathematical Morsels by Ross Honsberger (MAA, 1978)

#math​ #manim​ #visualproof​ #mathvideo​ #geometry #mathshorts​ #geometry #mtbos​ #animation​ #theorem​ #pww​ #proofwithoutwords​ #proof​ #iteachmath #dodecagon #area #dissection

To learn more about animating with manim, check out:

[vladimirrodriguez]

Summarizing the area of ​​the regular dodecagon is equal to 3/4 of the area of ​​the circumscribed square. What a beautiful visual proof

[ekoi]

Clarification: The dodecagon's area can be expressed as the sum of three squares, with each square having a side length equal to half the radius of the dodecagon.

[DeclanMBrennan]

Beauty was promised and beauty was delivered.

[kjag]

Your videos makes me want to relearn math sincerely. Someday I might. Keep making this videos. Appreciate it❤

[amitkasliwal]

Beautiful! The proof can be derived with Mid level Trigonometry. Area of Dodecagon expressed in terms of the radial drawn from the centre. The radii form 12 congruent isosceles triangles with Apex angles of 30 degrees each. Area of Dodecagon equals 12 times the area of the triangle. Using trigonometry the Radius r and side s can be shown to be related as r^2 = (2 + sqrt 3) s^2.
Area of each triangle in terms if side s equals s^2 (2 + sqrt 3)/4
Area of Dodecadron equals 12 times area of triangle = 3 s^2(2 + sqrt 3), which in terms of radius r = 3r^2

[anandakar]

Excellent, but yet to prove that those two brown and one purple triangles exactly fill up the gap in each quadrant (that those triangles have not been manipulated during animation).

[xbinarylol]

Mind blowing channel you got one more subscriber

[hrishikeshaggrawal]

beautiful piano rendition of the interstellar theme

[e]

This is calculated by the formula: sin(π/n)×cos(π/n)×n, where n is the number of sides

[walsoncastro]

Awesome. I did compute it and arrived at 12(cos 15)(sin 15) which is 3.

[orterves]

That's beautiful but I'm gonna have to write out the equations for a while to understand the proof of why those shapes really do fit into those spaces

[draido-dev]

if school show us things like this, everyone will be the next Einstein

[JJ-frki]

Zen Buddhist proof: I believe I’ve seen this proof in a book or a Scientific American article on a Buddhist geometric demonstration in Japan,
which in the 1600s used very general calculus methods—beyond Archimedean areas by exhaustion, and of course lacking algebra—but contemporaneous with Leibniz-Newton.

[eamonburns]

How do you know the equilateral triangles fit perfectly between the dodecagon and the corner of the square?

[duane]

What engineers think circles look like

[killianobrien]

Interesting how a shape close to a circle has an area of 3r², as the circle has area pi*r² and pi≈3

[rebtyxxz]

Lets just its approximately equal to pi

[googelman]

it looks cool but im still sticking to ap/2

[predrik]

I thiuht it was gonna be a proof that 1/4 of it fills 3/4 of the remaining square area but i guessed wrong lol
also is there a proof those triangles really fit like that

[GenericInternetter]

but how do you prove the triangles are the correct size?