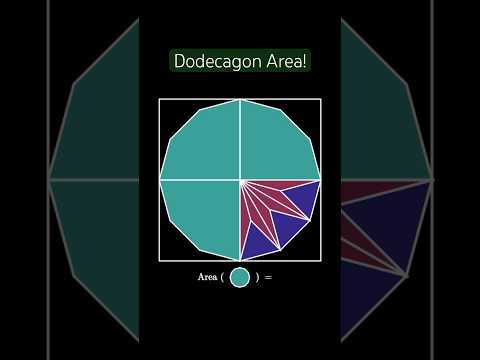
Area of dodecagon from a square!

This is a short, animated visual proof demonstrating that the area of a regular dodecagon inscribed in the unit circle has an area of exactly 3. #math​ #manim​ #visualproof​ #mathvideo​ #geometry #mathshorts​ #geometry #mtbos​ #animation​ #theorem​ #pww​ #proofwithoutwords​ #proof​ #iteachmath #dodecagon #area #dissection

Please consider subscribing if you like these videos.

Thanks to Matthew Scroggs for pointing me to the source.

See these videos for an alternate dissection proof of the same fact:

To learn more about animating with manim, check out:

[JohnSlack]

I think the whole world deserves to see these. They're really beautiful.

[adarshpradhan]

This is beautiful, I have tears in my eyes while seeing this magic of maths❤❤

[Scudboy]

This is why I find math to be beautiful.

[cicada.and.pomegranate]

This is a dodecagon not a dodecahedron

[ViniciusCortezao]

this manages to be beautiful, bizarre, strange, confusing, crazy and genius at the same time. I watched it 3 times to appreciate and understand

[TheDigiWorld]

Math really needs to be based on visuals rather than using million different equations to solve one problem

[abogmus]

RIP Robert Miles, never will i forget his music

[josecarloslozanopacheco]

Learning maths with the help of Robert Miles is priceless. Thank you :-)

[smileyp]

I feel like I'm learning math like the ancient Greeks!

[xjzgkke]

How do we know that the side of the triangle is equal to sqrt(3) ?

[palepoint]

The impressive thing about you that's you are always impressive 😮

[bathurstfreak]

There are 12 identical "slices of pie" of the dodecagon in the unit circle. The first slice of pie is 1 unit wide and 0.5 units high [ sin(30) = 0.5 ]. So the area of each triangle is 1 x 0.5 x 0.5 = 0.25 units so the full pie has area 12 x 0.5 = 3 units. Lovely way to demonstrate...

[MrMeszaros]

Okay - seems supersmooth.
BUT.
some steps would need a bit of explanation: like when folding the flaps in: why do they touch exactly?
How come do the blue flaps exactly fit the "star"?

Edit:
Okay, worked it out with paper and pencil. It just works. It turns out all those 30, 60, 45, 105 and 150 degrees just work out to make the top triangle a 60-60-60.
Also the bottom half-star turns to look like a square with three perfect triangles on its sides.
So in the end 150 + 60 + 90 + 60 = 360❤

[cerealkeepsyougoingeveryda]

Makes sense because a dodecagon circumscribed in a unit circle should have an area near Pi, right?

[GevinTheIdiot]

My brain has stopped working but this is beautiful

[MyHandleIsAplaceholder]

I wish you could save shorts into playlists

[balkeesshran]

Area of circle = area of square +12 small edge of (look like) semi circle is equal to 0.1415 ( From the value of π)
area of circle = 3+0.1415
= 3.1415

[davidnoll]

Cool animations, i think it’s a promising channel, but how do we know that the folds meet and make a perfect line segment in the middle?

[RNY]

Now turn a hexagon into any other polygon