Convex Relaxations in Power System Optimization: Computational Hardness (4 of 8)

Convex relaxations of the AC power flow equations have attracted significant interest in the power systems research community in recent years. This collection of videos provides a brief introduction to the mathematics of AC power systems, continuous nonlinear optimization, and relaxations of the power flow equations.

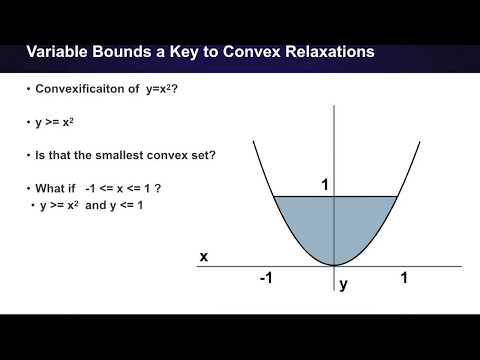
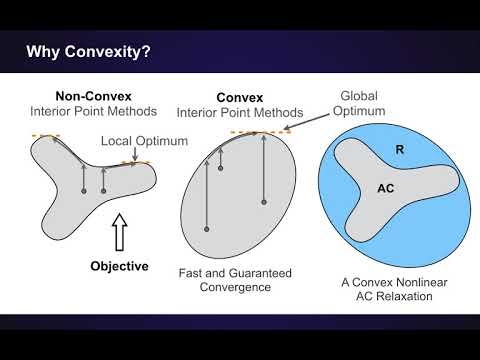
It is commonly acknowledged that the AC Optimal Power Flow problem is hard. This video provides a brief introduction to the concept of computational complexity, a theoretical field which provides a scientifically rigorous definition of what “hard” means. The NP-hardness of AC Optimal Power Flow is discussed and used to motivate the value of convexity in power system optimization.

References in the video:

LA-UR-18-26156