filmov
tv
Discrete Calculus
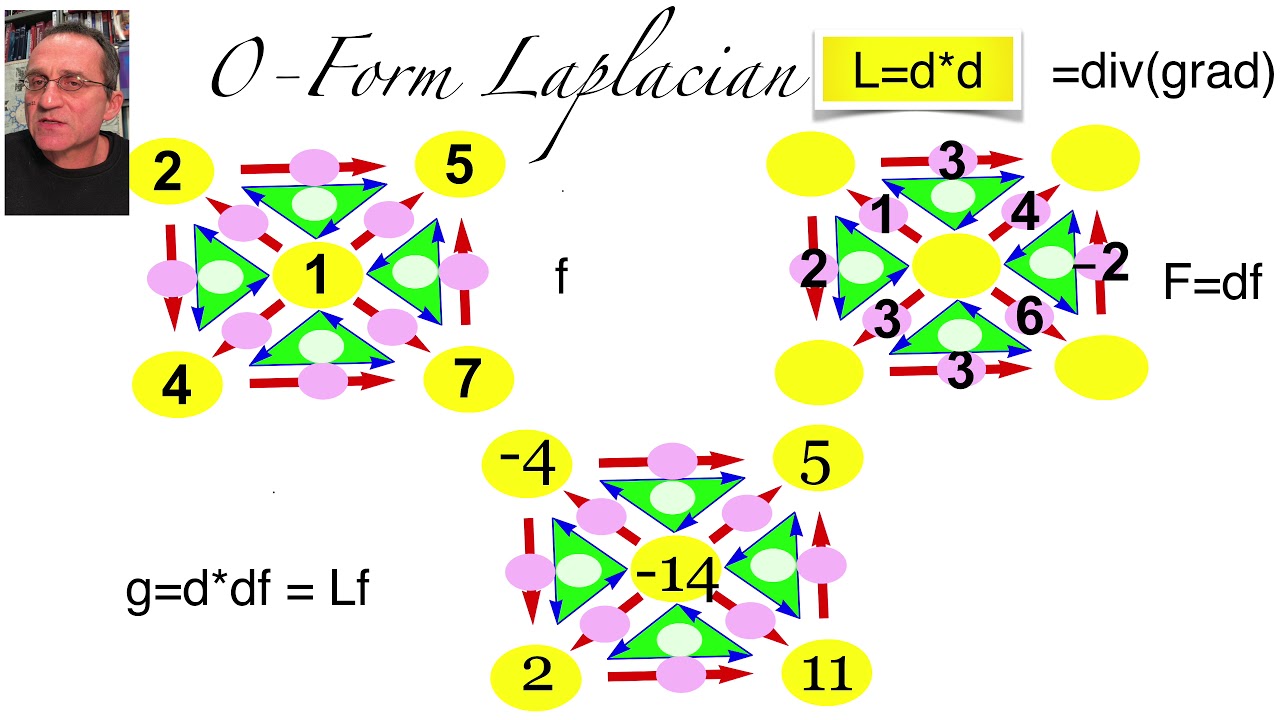
Показать описание
The Shadowy World of Umbral Calculus
Discrete Calculus - The Calculus of Finite Differences
Discrete Calculus: My favorite topic for a student seminar talk!
What is Discrete Calculus?
Why don't they teach Newton's calculus of 'What comes next?'
Discrete Calculus
Algorithmic Information Dynamics: A Discrete Calculus to Navigate Software Space
introduction to discrete calculus part 1
Calculus: When To Avoid The Quotient Rule for Derivatives
Rules for Discrete Derivatives, including the Falling Power Rule
ADS : Vol 1 : Chapter 2.4 : Discrete Calculus
An Introduction to 'sequences' and discrete calculus | Algebraic Calculus One | Wild Egg
Intro to Discrete Calculus
F. M. Atici, S. Chang: Introduction to h-Discrete Calculus
How to find the sum of the first n perfect squares? Use Discrete Integral Calculus Rules!
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Proving MY FAVORITE IDENTITY using DISCRETE DERIVATIVE
The Math Needed for Computer Science
Discrete Calculus I: Functions and Interpolation
ADS : Vol 1 : CHAPTER 2 : Continuous & Discrete Calculus
Introductory Discrete Mathematics by V.K. Balakrishnan
Calculus BLUE Trailer [2019-2020]
Semi-discrete Calculus Trailer
Why Shrek is in Your Calculus Textbook
Комментарии
 0:15:01
0:15:01
 0:20:14
0:20:14
 0:38:27
0:38:27
 0:05:24
0:05:24
 0:47:10
0:47:10
 0:07:53
0:07:53
 0:01:47
0:01:47
 0:13:12
0:13:12
 0:01:22
0:01:22
 0:15:14
0:15:14
 0:08:30
0:08:30
 0:27:25
0:27:25
 0:14:46
0:14:46
 0:23:43
0:23:43
 0:22:32
0:22:32
 0:00:38
0:00:38
 0:15:11
0:15:11
 0:14:54
0:14:54
 0:18:04
0:18:04
 0:01:05
0:01:05
 0:00:19
0:00:19
 0:01:37
0:01:37
 0:00:52
0:00:52
 0:00:43
0:00:43