filmov
tv
The Orthogonality of Hermite Polynomials
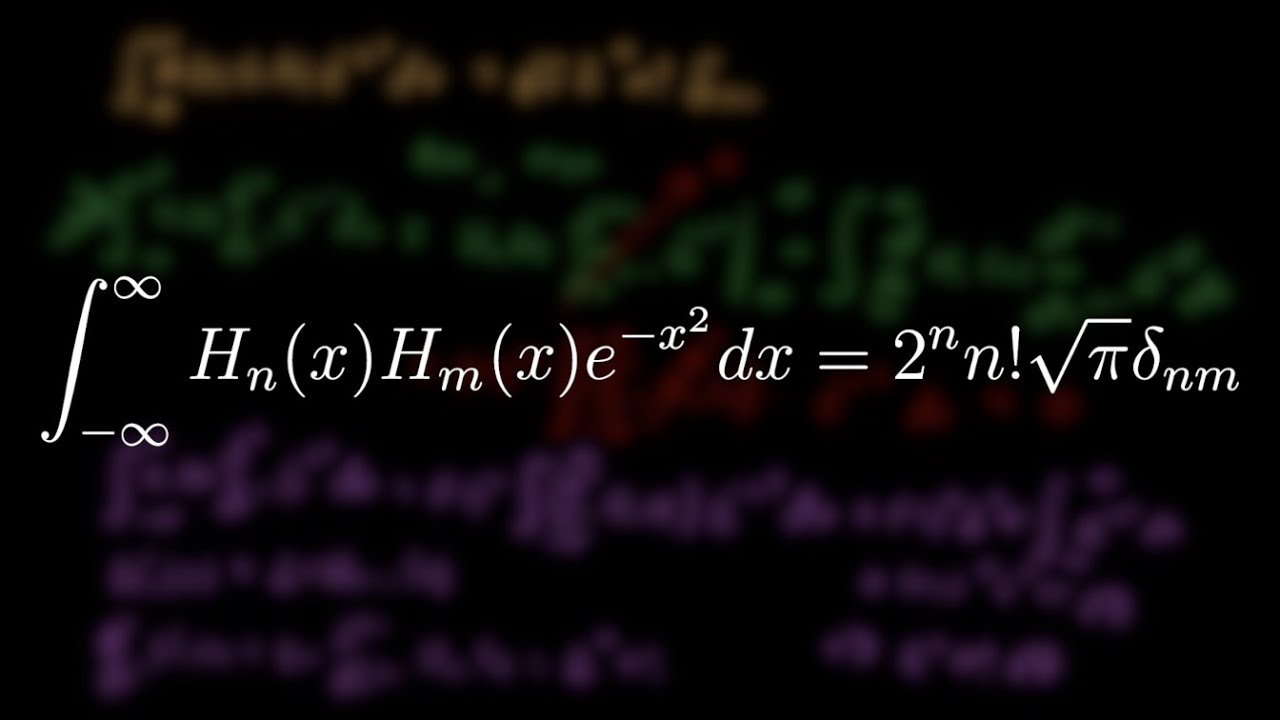
Показать описание
In this video I prove that Hermite polynomials are orthogonal with respect to a weighted inner product.
For more videos in this series, visit:
For more videos in this series, visit:
The Orthogonality of Hermite Polynomials
Orthogonality between Hermite polynomials
orthogonality relation of hermite polynomials
Orthogonality of Hermite Polynomial
Prove that the Hermite Polynomials are Orthogonal with respect to e^-x^2
The most useful polynomials you have never heard of.
ORTHOGONAL PROPERTY OF HERMITE POLYNOMIAL | ORTHOGONALITY OF HERMITE POLYNOMIAL | WITH EXAM NOTES |
Orthogonality of hermite polynomial/showing hermite Polynomials are orthogonal/normality condition..
Mathematical Physics- Special Functions: Hermite Polynomials- Orthogonal Properties
Hermite Polynomial Orthogonality proof
Orthogonal property of hermite polynomials. (MATH)
orthogonality of hermite polynomials in hindi
Orthogonality of Hermite Polynomials
Introduction to Hermite Polynomials
Mathematical Physics Lecture28: Hermite polynomials from orthogonality condition
Rodrigues and orthogonal for hermite
Rodrigues Formula for Hermite polynomials and Orthogonality
Orthogonality Relation For Hermite Polynomial Hn(x) || Lecture No 17 || Bengali
orthogonal property of hermite polynomial
Normalisation of Hermite polynomials
mod05lec46 - Hermite polynomials
Orthogonal prop Hermite polynomial
Degree Mathematics || Special Functions || Hermite polynomial -3
Orthogonal property of hermite polynomial notes 🥰🥰
Комментарии
 0:09:51
0:09:51
 0:08:14
0:08:14
 0:09:03
0:09:03
 0:33:30
0:33:30
 0:24:50
0:24:50
 0:20:26
0:20:26
 0:18:37
0:18:37
 0:18:09
0:18:09
 0:26:41
0:26:41
 0:06:24
0:06:24
 0:27:17
0:27:17
 0:07:38
0:07:38
 0:34:24
0:34:24
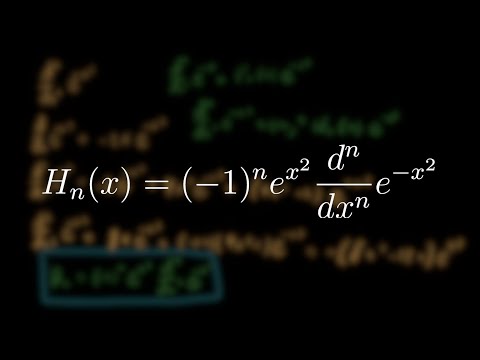 0:06:14
0:06:14
 0:20:53
0:20:53
 0:17:21
0:17:21
 0:10:21
0:10:21
 0:11:31
0:11:31
 0:00:16
0:00:16
 0:12:59
0:12:59
 0:22:37
0:22:37
 0:05:36
0:05:36
 0:13:14
0:13:14
 0:00:10
0:00:10