Rudin Illustrated Proof: Compact subsets of metric spaces are closed.

I illustrate and explain Walter Rudin’s proof for the following theorem from Principles of Mathematical Analysis:

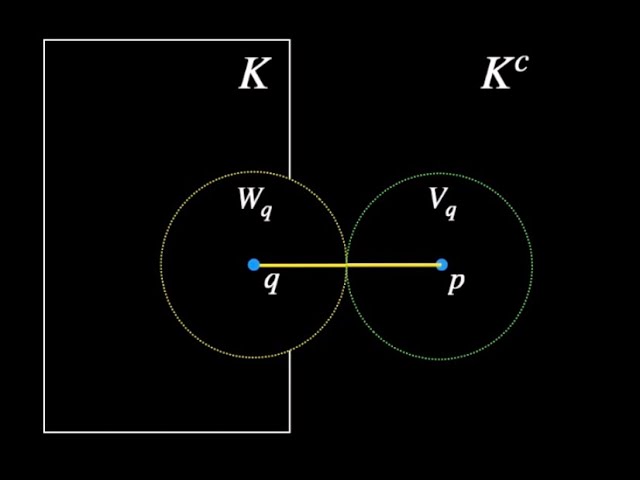
Theorem 2.34 Compact subsets of metric spaces are closed.

The argument is Rudin’s but the wording and illustrations are my own.

[tristanstaschik]

This is the best explanation of this proof I have ever seen. Thank you so much!

[samkirkiles]

This is awesome! This is one of my favorite proofs in the compactness section and its so cool to see the visualization of it like this.

[hannananan]

Wow, what a beautiful and simple way to prove this! Thank you! Both your channel and this video are underrated

[samkirkiles]

It would be so awesome if you did a visualization of every k-cell being compact. You could show the process of splitting into fourths each time and then applying the nested k-cell theorem. I subscribed :)

[suhanisoni]

U are so helpfullll. This must have taken sooo much efforts

[fanalysis]

I wanna be able to show that for a given x in W_q and y in V_q then d(x, y)>0 this would show disjointness of W_q and V_q right?