filmov
tv
Real Analysis 13 | Open, Closed and Compact Sets

Показать описание
Please consider to support me if this video was helpful such that I can continue to produce them :)
🙏 Thanks to all supporters! They are mentioned in the credits of the video :)
This is my video series about Real Analysis. We talk about sequences, series, continuous functions, differentiable functions, and integral. I hope that it will help everyone who wants to learn about it.
x
00:00 Intro
00:14 Recalling (epsilon-)neighbourhoods
01:33 Example: neighbourhoods
02:43 Definition open sets
04:00 Definition closed set
04:43 Examples
06:11 Criterion for checking closeness with the help of sequences
06:44 Example for the criterion
07:40 Definition compact sets
08:58 Credits
#RealAnalysis
#Mathematics
#Calculus
#LearnMath
#Integrals
#Derivatives
I hope that this helps students, pupils and others. Have fun!
(This explanation fits to lectures for students in their first and second year of study: Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)
Real Analysis 13 | Open, Closed and Compact Sets
Real Analysis 13 | Open, Closed and Compact Sets [dark version]
Real Analysis Ep 13: Open sets
Intro to Open Sets (with Examples) | Real Analysis
Open Covers, Finite Subcovers, and Compact Sets | Real Analysis
Open Covers Finite Subcovers
Identifying Open, Closed, and Compact Sets | Real Analysis Exercises
Intro Real Analysis 13: Prove Extreme Value Theorem, Intermediate Value Property, Uniform Continuity
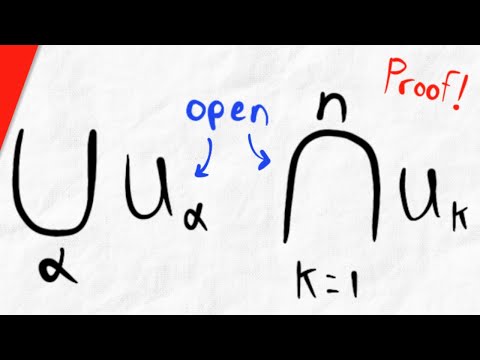
Proof for Unions and Intersections of Open Sets | Real Analysis
Real Analysis - Basic Topology (Open Sets, Closed Sets, Perfect Sets)
Real Analysis Final Exam Review Problems and Solutions (Topology on Metric Spaces)
13 1 The role of topology in real analysis
All About Closed Sets and Closures of Sets (and Clopen Sets) | Real Analysis
Learn Real Analysis With This Excellent Book
Real Analysis 13 - Completion of a Metric Space
11 years later ❤️ @shrads
Exploring Interior Point and Open Sets | Lecture-1 | Real Analysis
Real Analysis Course #13 - Sequences
Real Analysis 10 | Bolzano-Weierstrass Theorem
BEST DEFENCE ACADEMY IN DEHRADUN | NDA FOUNDATION COURSE AFTER 10TH | NDA COACHING #shorts #nda #ssb
Real Analysis: Metric Spaces:More about open sets. Lect. 13.#realanalysis #metricspace
Should I really Quit BDS ⁉️😣 | NEET 2024 or NEET 2025 👩⚕️ | Prachi Hooda : Doctor Siblings...
Countable sets l Real analysis
Real Analysis Lecture 13 Part 2: Open and closed sets
Комментарии
 0:09:28
0:09:28
 0:09:15
0:09:15
 0:50:48
0:50:48
 0:08:58
0:08:58
 0:13:58
0:13:58
 0:05:01
0:05:01
 0:07:54
0:07:54
 0:36:37
0:36:37
 0:08:07
0:08:07
 0:22:53
0:22:53
 1:19:57
1:19:57
 0:26:16
0:26:16
 0:11:48
0:11:48
 0:10:40
0:10:40
 0:22:25
0:22:25
 0:00:11
0:00:11
 0:10:04
0:10:04
 0:02:59
0:02:59
 0:06:12
0:06:12
 0:00:15
0:00:15
 0:27:50
0:27:50
 0:00:13
0:00:13
 0:00:29
0:00:29
 0:22:54
0:22:54