filmov
tv
Limits at infinity of quotients with square roots (even power) | AP Calculus AB | Khan Academy

Показать описание
Limit at infinity of rational expression with radical.
AP Calculus AB on Khan Academy: Bill Scott uses Khan Academy to teach AP Calculus at Phillips Academy in Andover, Massachusetts, and heÕs part of the teaching team that helped develop Khan AcademyÕs AP lessons. Phillips Academy was one of the first schools to teach AP nearly 60 years ago.
For free. For everyone. Forever. #YouCanLearnAnything
Limits at infinity of quotients with square roots (even power) | AP Calculus AB | Khan Academy
Limits at infinity of quotients (Part 1) | Limits and continuity | AP Calculus AB | Khan Academy
How To Find The Limit At Infinity
Limits at infinity of quotients with trig | Limits and continuity | AP Calculus AB | Khan Academy
AP Calculus AB - Limits at Infinity of Quotients
Limits at Infinity & Horizontal Asymptotes
Limits at infinity of quotients with square roots (odd power) | AP Calculus AB | Khan Academy
Limits at infinity of quotients with trig (limit undefined) | AP Calculus AB | Khan Academy
This is a very famous limit
Limit at Infinity of a Quotient with a Square Root: 3 Methods
The fastest way to evaluate Limits at infinity of quotients.
Learn how to evaluate a limit at infinity
Determine Limits at Infinity of Quotients Involving Exponential Terms: 2 Methods (Ex 1)
Determine Limits at Infinity of Quotients Involving Exponential Terms: 2 Methods (Ex 3)
Limits at Infinity (Rational square-root function as x approaches negative Infinity)
Limits at infinity of quotients (Part 2) | Limits and continuity | AP Calculus AB | Khan Academy
Limits at Infinity Challenge with Quotient of Squareroots functions
C Limits at Infinity with Quotients
Limit solving (limit at infinity of a rational function)
Determine Limits at Infinity of Quotients Involving Exponential Terms: 2 Methods (Ex 2)
Evaluating Limits at Infinity of Rational Functions with Square Roots (Example)
Limits at Infinity
Infinite Limits With Equal Exponents (Calculus)
Evaluate a limit at infinity with a radical in denominator
Комментарии
 0:03:36
0:03:36
 0:04:07
0:04:07
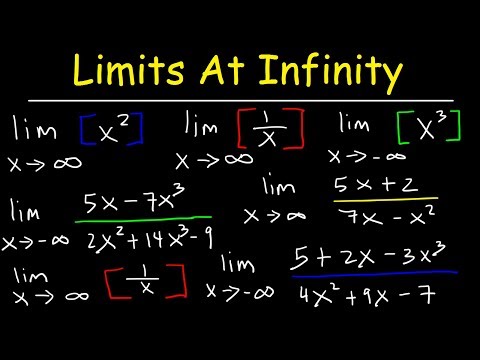 0:13:14
0:13:14
 0:03:03
0:03:03
 0:10:20
0:10:20
 0:19:24
0:19:24
 0:05:14
0:05:14
 0:02:20
0:02:20
 0:00:48
0:00:48
 0:03:57
0:03:57
 0:00:53
0:00:53
 0:01:40
0:01:40
 0:04:32
0:04:32
 0:07:46
0:07:46
 0:09:52
0:09:52
 0:04:33
0:04:33
 0:03:03
0:03:03
 0:09:32
0:09:32
 0:01:00
0:01:00
 0:05:29
0:05:29
 0:04:53
0:04:53
 0:09:54
0:09:54
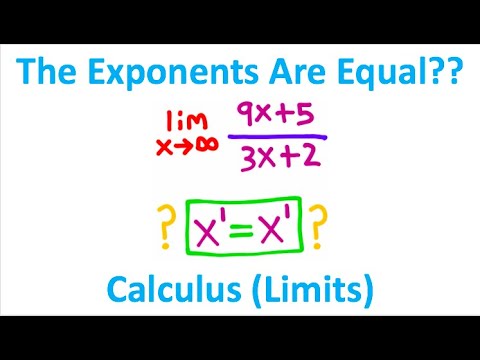 0:00:49
0:00:49
 0:03:14
0:03:14