filmov
tv
Quaternion Julia Set Shape Optimization

Показать описание
We present the first 3D algorithm capable of answering the question: what would a Mandelbrot-like set in the shape of a bunny look like? More concretely, can we find an iterated quaternion rational map whose potential field contains an isocontour with a desired shape? We show that it is possible to answer this question by casting it as a shape optimization that discovers novel, highly complex shapes. The problem can be written as an energy minimization, the optimization can be made practical by using an efficient method for gradient evaluation, and convergence can be accelerated by using a variety of multi-resolution strategies. The resulting shapes are not invariant under common operations such as translation, and instead undergo intricate, non-linear transformations.
Quaternion Julia Set Shape Optimization
The Infinite Beauty and Mystery of the Mandelbrot Set
Quat_01.mov
On Julia Sets
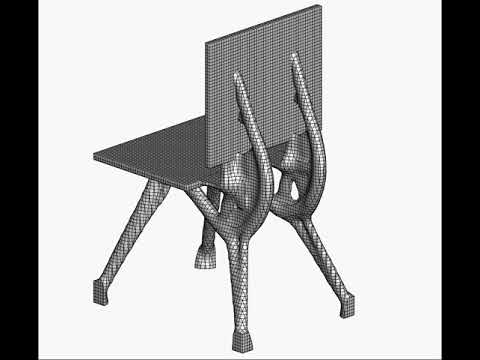
Level set based shape optimization using trimmed H8 meshes - Ex #3: Chair problem
A Study of 4D Julia Sets; Iterations of Z=Z_ + K in the Quaternions by Dan Sandin
Quaternion Mandelbrot Set Rotated in XW-plane
'Solar Spindle' A Quaternion Julia Set
Quaternion julia set
Julia Set Fractal Tessellation - Algorithmic Art
New Julia sets
A Shape Modulus for Fractal Geometry Generation
4D rotating hypercomplex Quaternion Julia Set
quaternion julia
Rotating 4D Quaternion Julia set
4D Quaternion Hypercomplex Mandelbrot Set
4D Quaternion Julia set
Julia Quaternion
Julia set of a Dragon
gpu quaternion julia
Three-dimensional slices of a four-dimensional quaternion Julia set
Quaternion Mandelbrot set rotated in XW-plane
Julia Sets - Spiraling Through Mandelbrot Set
Quaternion fractal
Комментарии
 0:04:09
0:04:09
 0:00:35
0:00:35
 0:00:32
0:00:32
 0:29:02
0:29:02
 0:00:21
0:00:21
 0:03:32
0:03:32
 0:00:31
0:00:31
 0:00:56
0:00:56
 0:00:52
0:00:52
 0:00:06
0:00:06
 0:00:33
0:00:33
 0:02:20
0:02:20
 0:04:01
0:04:01
 0:00:05
0:00:05
 0:04:49
0:04:49
 0:00:41
0:00:41
 0:00:58
0:00:58
 0:01:52
0:01:52
 0:00:07
0:00:07
 0:00:59
0:00:59
 0:01:20
0:01:20
 0:01:02
0:01:02
 0:01:20
0:01:20
 0:00:55
0:00:55