filmov
tv
the parabolic trig functions

Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
the parabolic trig functions
Hyperbolic Functions: Definitions, Identities, Derivatives, and Inverses
Trig Visualized: One Diagram to Rule them All (six trig functions in one diagram)
Introduction to Hyperbolic Trig Functions
The applications of hyperbolic trig | Why do we even care about these things?
The Secret Connection between Hyperbolic and Trigonometric Functions...
The Graphs of Hyperbolic Trig Functions
Everything You Need To Know About Parabolas In 2 Minutes
Arc Length Along Parabola 1: Base Case
Derivatives of Hyperbolic Functions
Trig and Suspension Bridge with parabolas
How to rotate any graph by any angle
Before JEE vs After JEE 😍 | My Transformation💔 | IIT Motivation|Jee 2023 #transformation #iit #viral...
Trigonometric and Hyperbolic Functions of Complex Numbers (Math/Filipino Math)
The equation for Gateway Arch in St. Louis #math #parabola #stlouis #catenary
Parabola Find Vertex, Focus, Directrix, and Graph
Derive the Hyperbolic Equation - Hyperbolic Trigonometric Function - #Calculus by #Moein
MAC1114 Lecture Sect 6.3 Properties of Trig Functions
Trigonometric Function Graph and Transform Understand All About Cosine MCR3U IBSL AP Mathematics
How to Properly Type Trigonometric Functions in a TI-84 Plus CE Calculator
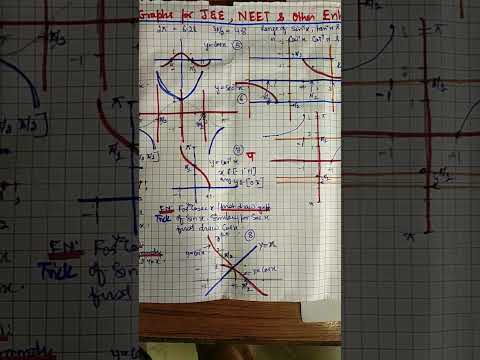
GRAPHS IIT JEE NEET ENTRANCE TRIGO SIN COS SEC COSEC COT TAN Their INVERSE PARABOLA EXPONENTIAL LOG
The Derivatives of Inverse Trigonometric Functions | Basic Calculus
Pi for parabolas!!
Comparing Forms of Trigonometric Functions: Transformations
Комментарии
 0:23:03
0:23:03
 0:07:34
0:07:34
 0:04:15
0:04:15
 0:08:21
0:08:21
 0:14:45
0:14:45
 0:17:36
0:17:36
 0:23:49
0:23:49
 0:02:00
0:02:00
 0:10:05
0:10:05
 0:10:08
0:10:08
 0:01:55
0:01:55
 0:16:10
0:16:10
 0:00:20
0:00:20
 0:19:23
0:19:23
 0:00:50
0:00:50
 0:08:33
0:08:33
 0:02:30
0:02:30
 1:31:15
1:31:15
 0:46:20
0:46:20
 0:02:23
0:02:23
 0:00:15
0:00:15
 0:18:35
0:18:35
 0:00:42
0:00:42
 0:09:00
0:09:00